Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Propagació de l'error
Error propagat amb funcions de més d'una variable
Introducció «
Es calcula la incertesa d'una funció de n variables u(x1, ..., xn) on les variables tenen incerteses δk. Es trobarà que la funció avaluada en el punt A = (x10, x20, ..., xn0) té la incertesa
δu = |c1| δ1 +|c2| δ2 + ... + |cn| δn.
amb
S'usa com exemple en aquest tema, la mesura de la relació càrrega/massa dels electrons a partir de la trajectòria en un camp magnètic.
Motivació: La mesura de la relació e/m «
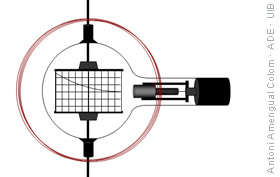La trajectòria d'un electró dins un camp magnètic uniforme és circular. El radi depèn de la intensitat del camp magnètic, la velocitat dels electrons i la relació u entre la càrrega i la massa dels electrons. Llavors, el valor de u es pot calcular mesurant el radi de la trajectòria dels electrons que es mouen amb una mateixa velocitat dins un camp magnètic d'intensitat coneguda.
A la figura adjunta s'han dibuixat els fils d'una bobina (cercles de color) i un tub que emet electrons al buit, amb una velocitat determinada pel potencial aplicat al tub. A l'altra banda del tub hi hauria una bobina igual. La parella de bobines coaxials i separades s'anomenen bobines de Helmholtz i donen un camp bastant uniforme sobre l'eix a prop de la zona central. Un dispositiu d'aquest tipus és adient per a un laboratori docent on només es pretén reproduir el valor acceptat
u ≡ e/m = 1.76×1011 C/kg.
La placa central que hi ha dins el tub, amb un reticle regular amb marques principals cada centímetre, està lleugerament girada i intercepta el feix d'electrons. Tots els electrons del feix segueixen una trajectòria circular, però com que el feix és ampla, uns electrons impacten sobre la placa més a prop del canó i altres més enfora. La placa brilla on hi ha impactes i, per l'immens nombre d'electrons emesos, apareix una línia brillant que mostra la trajectòria que tendrien els electrons si la placa no hi fos.
Per a un determinat dispositiu experimental, la relació càrrega/massa s'ha de calcular amb la fórmula(1)
on μ0 és la permeabilitat del buit (4π 10-7 N A–2) i N és el nombre de voltes del fil d'una de les bobines que generen el camp magnètic. Se suposarà que N = 103. Les altres variables de la fórmula i els valors són:
D = 21.5 ± 0.2 cm, diàmetre de la bobina,
V = 1.16 ± 0.01 kV, diferència de potencial que fixa la velocitat dels electrons,
d = 92.8 ± 0.2 mm, diàmetre de la trajectòria dels electrons,
I = 2.87 ± 0.04 A, corrent elèctric de la bobina.
Amb aquests valors es calcula
u = 1.76×1011 C/kg.
La discrepància amb el valor acceptat és inferior a la tercera xifra significativa. Cal demanar-se si es té una mesura molt ben feta o si es tracta d'una coincidència afortunada. Per respondre, s'ha de determinar la incertesa del valor calculat a partir de les incerteses de cada una de les quatre variables mesurades: D, V, d i I. Aquest és el tipus de càlcul que es descriurà aquí.
De manera general, es considerarà una funció de n variables,
u = u(x1, x2, ..., xn),
i es calcularà què val δu quan les variables xk tenen incerteses δk.
La incertesa a partir dels valors mínim i màxim de la funció «
Cada una de les variables x1, x2, ..., xn de les que depèn una funció u tendrà un valor i una incertesa
xk = xk0 ± δk.
Per a cada variable tendrem tres valors a tenir en compte
xk0 − δk,
xk0,
xk0 + δk.
Es poden fer 3n combinacions usant un valor dels tres de cada variable. Els valors mínim i màxim que resultin de les combinacions donaran l'estimació de la incertesa del valor de la funció.
Per a n = 4, el nombre de combinacions ja són vuitanta-una i el procediment no és massa eficient. Normalment, però, es poden identificar els valors que donaran el mínim i el màxim mirant si la funció creix o decreix al modificar cada una de les variables mantenint constants les altres.
Exemple amb la mesura de la relació u = e/m «
En el càlcul de la relació càrrega/massa hi intervenen quatre variables amb incertesa: D, V, d i I. Les dues primeres variables estan en el numerador del quocient que dóna u i les altres dues, en el denominador.
La intensitat del corrent elèctric que circula per les bobines del sistema descrit a la introducció s'espera que estigui dins l'interval [2.45 A, 2.53 A]. Com que la intensitat es troba en el denominador, u augmenta si el valor de la intensitat disminueix; el mateix passa amb el valor del diàmetre de la trajectòria dels electrons; però és al revés amb el diàmetre de les bobines i el voltatge que dóna velocitat als electrons. Els valors més grans de D i V, combinats amb els més petits de d i I, donen el valor més gran que caldria esperar,
El valor més petit s'obtendrà amb
Usant la distància entre els valors extrems com el doble de la incertesa del valor central, s'escriu
u = (1.77 ± 0.10)×1011 C/kg.
La incertesa relativa és del 6%.
Les abscisses dels segments verticals de la Fig. 1 il·lustren la distribució dels vuitanta-un valors que surten combinant els tres valors xk0 − δk, xk0 i xk0 + δk de cada variable. Les línies vermella i verda són els valors mínim i màxim.
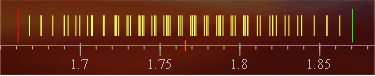
Figura 1. Els vuitanta-un valors de la funció u calculats amb les combinacions dels valors centrals i extrems de les seves quatre variables.
La distribució de les marques entre els extrems de la Fig. 1 no és uniforme. Com que les mesures de les variables són independents, la probabilitat que totes les variables del numerador estigui sobrevalorades i les del denominador infravalorades és més petita que algunes estiguin sobrevalorades i les altres infravalorades. Aquesta idea es desenvolupa amb l'anàlisi estadístic dels errors (cas de la suma de dues variables).
La incertesa del producte i el quocient de variables
«
Moltes relacions entre variables físiques es poden escriure en la forma
u = u(x1, x2, ..., xn) = x1a1 x2a2 ··· xnan
on {ak} és un grup de constants positives o negatives.
Exemples »
En aquests casos, en lloc de calcular la incertesa δu directament és més fàcil calcular la incertesa relativa δu/u. El motiu és que la incertesa relativa de u és igual a la incertesa absoluta del logaritme neperià de u,
el producte es converteix en la suma de logaritmes i el quocient, en resta,
ln(u) = a1 ln(x1) + a2 ln(x2) + ... + an ln(xn).
La incertesa de ln(u) és pot calcular amb la propagació de la incertesa deguda a operacions bàsiques com la del logaritme d'una variable, el producte d'una constant per una variable i la suma de dues variables (dues són suficients perquè la suma de n variables és pot fer sumant n – 1 termes de dos en dos):
Suma amb només dos sumands »
Exemple: u = s r v
«
La incertesa del producte de dues variables es va calcular en un tema anterior. Ara la incertesa de
u = s r v
es pot calcular de dues maneras.
Mètode 1. Amb la regla bàsica del producte de dues variables aplicada dos pics. Primer es pot escriure
δu = |r v| δs + |s| δrv
Però
δrv = | v | δr + | r | δv.
Així que
δu = | r v | δs + | s v | δr + | s r | δv.
Dividint tot per u queda
Mètode 2. Aplicant el logaritme neperià.
ln(u) = ln(s r v) = ln(s) + ln(r) + ln(v).
La incertesa d'una suma és la suma d'incerteses
La incertesa del logaritme neperià és igual a la incertesa absoluta de l'argument. Per tant
Aquest és el mateix resultat obtingut amb el primer mètode.
Exemple amb la mesura de la relació u = e/m
«
L'expressió que dóna la relació càrrega/massa dels electrons té diversos termes constants i no fa falta tenir-los en compte per calcular la incertesa a partir de la del logaritme. Una avantatge addicional del càlcul de la incertesa amb el logaritme és que cada variable es pot expressar en les unitats més adients. Diverses variables que representen longituds poden expressar-se en unitats diferents perquè el quocient entre la incertesa i el valor d'una variable no tendrà unitats. En el càlcul del valor de la relació càrrega/massa
és necessari expressar el diàmetre de la bobina i el diàmetre de la trajectòria dels electrons amb la mateixa unitat de longitud, però per calcular la incertesa de l'expressió amb el logaritme, es pot posar D en centímetres i d en mil·límetres. Les unitats poden ser distintes. Per exemple:
La incertesa relativa de u és del 6% i l'absoluta,
δu = 0.059 u = 0.059×(1.76×1011 C/kg) = 0.10×1011 C/kg.
Un cas senzill (que s'aplicarà al cas general)
«
La incertesa de
u = u(x1, x2) = c1 x1 + c2 x2
on c1 i c2 són dues constants de signe arbitrari es determina de manera directa amb les fórmules demostrades per a la incertesa propagada amb operacions bàsiques. La combinació lineal és com la suma de dues variables cada una de les quals és igual a una constant per una variable. La incertesa d'una variable igual a una altra multiplicada per una constant és una operació bàsica i la suma de dues variables, també. Llavors
δu = |c1| δ1 + |c2| δ2.
Aquesta fórmula es pot aplicar per determinar la incertesa de
u = u(x1, x2, ..., xn) = c0 + c1 x1 + ... + cn xn
on hi ha n constant ci. La suma de n termes es pot fer amb n – 1 sumes on només intervenen dos sumands. Com que la incertesa del terme constant c0 és nul·la, es té
δu = |c1| δ1 +|c2| δ2 + ... + |cn| δn.
Aquest resultat és senzill però s'aplica al càlcul de la incertesa de qualsevol funció com es veurà en el darrer apartat d'aquest tema.
La incertesa a partir de les derivades parcials
«
La sèrie de Taylor de primer ordre de la funció u en el punt A = (x10, x20, ..., xn0) és
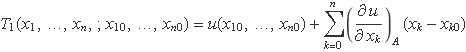
(A és un punt en un espai de n dimensions).
Si la incertesa no és molt gran, es pot usar la sèrie de Taylor en lloc de la funció. Les derivades estan avaluades en el punt A i donen valors constants ck. L'expressió anterior es pot escriure en la forma
u ≈ T1 = c0 + c1 x1 + ... + cn xn.
El valor de c0 no és rellevant; el de les altres constants és
Si les variables canvien poc i els valors ck no són nuls, la funció u es pot calcular amb una combinació lineal i la incertesa d'una combinació lineal, com s'ha vist en aquest tema, és
δu = |c1| δ1 +|c2| δ2 + ... + |cn| δn.
Exemple amb la mesura de la relació u = e/m
«
A partir de la funció
i els valors especificats abans, es calculen les derivades parcials i es troba
Amb aquests valors es té
δu = |c1| δ1 +|c2| δ2 + ... + |cn| δn = 0.10 × 1011,
un valor com el que ja s'havia obtingut i permetia escriure
u = (1.77 ± 0.10)×1011 C/kg.
Un altre exemple
«
Sigui x = 21 ± 1 i y = 35 ± 2. Es vol calcular u = ln(y + x2):
u = 6.1654,
u = 6.17 ± 0.09
