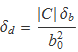La longitud del perímetre i l'àrea de la superfície d'una taula rectangular es pot determinar mesurant les longituds de dos costats veïns. Els errors de les dues mesures (tal vegada de l'ordre del mil·límetre) es propagarà al perímetre, l'àrea i qualsevol altre valor que es calculi a partir dels valors mesurats. Els errors es propaguen amb totes les operacions matemàtiques fetes amb números que no es coneixen exactament. En aquest tema es comença a estudiar com és la propagació amb operacions bàsiques.

En el que segueix cal distingir entre la variable mesurada, el seu valor i l'error. Per exemple, la variable pot ser l'altura d'un objecte identificada amb la lletra h, Per indicar els valors de l'altura i l'error sense especificar-los amb números concrets, el primer valor s'identificarà amb h₀ i el segon, amb la lletra grega δ i el subíndex h: δ_h.

En els casos següents a i b representaran dues variables que tenen valors coneguts i incerteses determinades,

a = a₀ ± δ_a,
b = b₀ ± δ_b.

Es vol determinar la incertesa del valor de la suma

s = a + b.

Els valors mínim i màxim que podria tenir s són

s_min = (a₀ – δ_a) + (b₀ – δ_b) = (a₀ + b₀) – (δ_a + δ_b),

s_màx = (a₀ + δ_a) + (b₀ + δ_b) = (a₀ + b₀) + (δ_a + δ_b).

El valor de la suma estarà entre aquests dos extrems. Es pot escriure

s = (a₀ + b₀) ± (δ_a + δ_b).

Per tant,

Exemple »

Es vol determinar la incertesa del valor de la resta

r = a – b.

Es calcularan els valors mínim i màxim que podria tenir r. El valor mínim s'obtendrà quan el màxim de b es resti al mínim de a. El valor màxim s'obtendrà quan el mínim de b es resti al màxim de a:

r_min = (a₀ – δ_a) – (b₀ + δ_b) = (a₀ – b₀) – (δ_a + δ_b),

r_màx = (a₀ + δ_a) – (b₀ – δ_b) = (a₀ – b₀) + (δ_a + δ_b).

El valor de la resta estarà entre aquests dos extrems. Es pot escriure

r = (a₀ – b₀) ± (δ_a + δ_b).

Per tant,

Les incerteses de a i b s'han de sumar encara que l'operació hagi estat una resta.

Exemple »

Es vol determinar la incertesa del valor del producte

p = a b.

Per determinar la incertesa es calcularan els valors mínim i màxim del producte. Primer, se suposarà que els valors numèrics de les variables a i b són tots dos positius. Així,

p_min = (a₀ – δ_a) (b₀ – δ_b) = a₀ b₀ – a₀ δ_b – b₀ δ_a + δ_a δ_b,  

p_màx = (a₀ + δ_a) (b₀ + δ_b) = a₀ b₀ + a₀ δ_b + b₀ δ_a + δ_a δ_b.

El motiu d'haver de saber els signes dels valors de a i b per determinar el màxim i el mínim del producte quedarà clar amb un exemple. Si els valors que representen a i b són 39 i 29, respectivament, amb una incertesa d'una unitat, el valor màxim del producte s'obtendrà multiplicant els valors augmentats amb la incertesa (39 + 1)(29 + 1) = 1200; però si els valors que representen a i b són –39 i –29, el valor màxim del producte s'obtendrà multiplicant els valors minvats amb la incertesa, (–39 – 1)(–29 – 1) = 1200.

El valor central i la incertesa són

En molts de casos

δ_a δ_b ≪ a₀ b₀

de manera que

p₀ ≈ a₀ b₀

i la incertesa val

δ_p = b₀ δ_a + a₀ δ_b.

Si els valors numèrics de les variables a i b són tots dos negatius, el signe es cancel·la al multiplicar i la incertesa serà la mateixa que si el càlcul es fes amb a i b en valor absolut. Per tant,

Si un dels dos valors és negatiu, el resultat del producte és negatiu. Es pot suposar que tots els càlculs es fan amb els valors absoluts i que el resultat i la incertesa es multipliquen per -1 al final. Els noms de p_màx i p_min estaran intercanviats, però δ_p tendrà el mateix valor.

Dividint els dos membres per s'obté una forma bastant utilitzada: La incertesa relativa del producte és igual a la suma de les incerteses relatives en valor absolut:

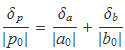
Exemple »

Es vol determinar la incertesa del valor de la divisió

d = a / b.

Per determinar la incertesa s'han de calcular els valors mínim i màxim que podria tenir d. Com ja ha passat amb el producte, la incertesa només depèn dels valors absoluts de les variables. Aquí es calcularà la incertesa de la divisió suposant que a i b tenen valors positius i el resultat final s'expressarà amb valors absoluts.

Com exercici es pot repetir explícitament la deducció feta a continuació suposant que una de les variables pren un valor negatiu.

El valor mínim de s s'obtendrà quan el mínim de a es divideixi pel màxim de b:

El valor màxim de s s'obtendrà quan el màxim de a es divideixi pel mínim de b:

El valor central i la incertesa són

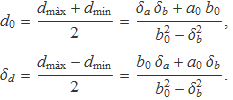
En molts de casos es compleix

δ_a δ_b ≪ a₀ b₀,

δ_b² ≪ b₀²,

de manera que

d₀ = a₀ / b₀.

i la incertesa val

Si alguna de les variables o les dues tenen valors negatius, la incertesa es calcula amb la mateixa expressió usant el valor absolut de les variables

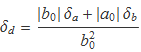
Dividint els dos membres per s'obté una forma bastant utilitzada: La incertesa relativa de la divisió és igual a la suma de les incerteses relatives en valor absolut. L'expressió és formalment igual a l'expressió de la incertesa del producte:

Exemple »

El títol d'aquest apartat podria ser simplement «suma o multiplicació per una constant» perquè restar C és el mateix que sumar –C i dividir per C és el mateix que multiplicar per C^–1.  

Al considerar una constant C amb les operacions

s = a + C,

r = a – C,

p = C a,

d = a / C,

es poden aplicar els resultats dels apartats anterios amb b = C i δ_b = 0. Així, sumar o restar una constant no modifica la incertesa, i multiplicar o dividir per la constant, multiplica o divideix la incertesa en la mateixa proporció:

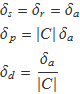
Les constants físiques com la de gravitació universal o la de Planck s'han de mesurar i tenen una incertesa, però en determinats càlculs es pot negligir perquè és molt més petita que la d'altres termes.

L'expressió

deduïda per a la incertesa d'una divisió, aplicada al cas a = C, dóna

Exemple »