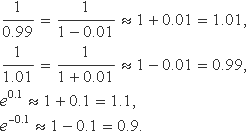Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Propagació de l'error
Sèries de Taylor
Funcions d'una variable «
Figura 1. Aproximació d'una funció (línia groga) per una sèrie de Taylor al voltant del punt marcat i truncada fins al grau indicat sobre el gràfic (línia verda).
La sèrie de Taylor en el punt x0 d'una funció f(x) diferenciable és
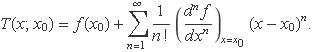
La sèrie amb els dos primers termes del sumatori escrits explícitament és
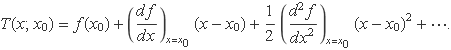
Quan la serie es calcula en el punt x0 = 0, es diu sèrie de Maclaurin,
![]()
Una de les aplicacions de les sèries de Taylor és usar-les truncades en substitució de la funció original. La sèrie truncada és un polinomi el qual pot simplificar alguns tractaments analítics. La diferència entre els valors de la funció i la sèrie truncada fins el terme de grau m és
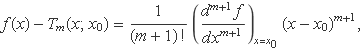
on xc és un valor entre x i x0.
La Fig. 1 mostra els gràfics d'una funció i les sèries de Taylor truncades a graus diferents. Es mostren les sèries per a dos valors de x0.
Algunes sèries de Maclaurin usades freqüentment són
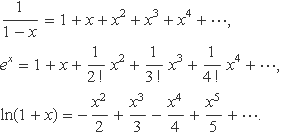
Nota »
La Fig. 2 mostra els gràfics de les sèries de Maclaurin de (1–x)-1 truncades a graus diferents.
Figura 2. Representació de la funció 1/(1-x) (línia groga) i la sèrie de Maclaurin truncada (línia verda) a diferents graus.
Funcions de dues variables
 «
«
La sèrie de Taylor d'una funció de dues variables f(x, y) en el punt (x0, y0) truncada a primer ordre és
![]()
La Fig. 3 mostra la representació de la funció de dues variables com una superfície que a cada punt (x, y) està a l'altura z = f(x, y). La sèrie de Taylor truncada a primer ordre dóna el pla tangent a la funció en el punt (x0, y0).
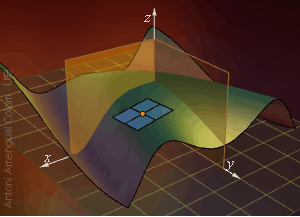
Figura 3. Pla tangent en el punt taronja a la superfície ondulada representativa d'una determinada funció de dues variables.
Funcions de n variables
 «
«
La sèrie de Taylor també es pot definir per a una funció de n variables f(x1, x2, ..., xn). La sèrie en el punt A = (x10, x20, ..., xn0) truncada a primer ordre és

Donada la funció de tres variables
![]()
la sèrie truncada a ordre 1 en el punt A tal que P = P0, v = v0 i θ = θ0 es determina calculant
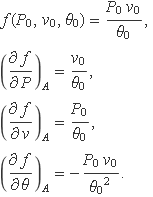
Amb aquestes expressions es tendrà l'aproximació
![]()
Per exemple, amb P0 = 2.00, v0 = 5.0 i θ0 = 273, els valors exacte i aproximat de f(2.01, 5.1, 274) són 0.03819636 i 0.03819319, respectivament. Els decimals diferents s'han escrit en gris.