
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Propagació de l'error
Funcions d'una variable
Introducció «
La incertesa del valor d'una funció u(x) deguda a la incertesa δx del valor x0 de l'argument és
δu = (umàx – umín) / 2,
on umàx i umín són els valors màxim i mínim de la funció dins l'interval [x – δx, x + δx]. Però la incertesa δu es pot calcular a partir de la derivada de la funció si δx és suficientment petit. A continuació se'n dóna una justificació gràficament.
Casos segons com sigui la funció en el punt central
 «
«
Per calcular la incertesa del valor d'una funció, s'ha de saber si la funció és monòtona en tot l'interval x0 ± δx, o si té un màxim, un mínim o un punt d'inflexió horitzontal.
Sense perdre generalitat, basta analitzar els casos on la funció és monòtona creixent, té un màxim o té un punt d'inflexió horitzontal dins l'interval perquè la incertesa de v(x) = –u(x) és la mateixa que la de u; però si la funció u és decreixent o té un mínim, la funció v serà creixent o tendrà un màxim.
La funció és creixent
 «
«
1)
La línia groga representa una determinada funció u(x).
El punt blanc és el valor central de la variable x i el segment verd representa l'interval entre el mínim i el màxim de la variable.
Figura 1. Explicació del càlcul de l'error d'una funció f(x) on la funció és creixent.
La funció té un màxim
 «
«
1)
La línia groga representa una determinada funció u(x) al voltant d'un màxim.
El punt blanc és el valor central de la variable x i el segment verd representa l'interval entre el mínim i el màxim de la variable.
Interessa determinar la incertesa sobre el valor de la funció u(x).
Figura 2. Explicació del càlcul de l'error d'una funció f(x) en un punt x0 prop d'un màxim.
La funció té un punt d'inflexió horitzontal
 «
«
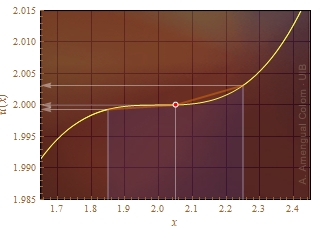
Figura 3. Funció f(x) amb el punt x0 prop d'un punt d'inflexió.
La derivada de la funció té un valor proper a zero a x0, llavors la incertesa s'ha de calcular directament a partir dels valors de la funció en els extrems de l'interval de x.
Aplicacions
 «
«
A continuació es determinen les incerteses calculades en el tema d'operacions bàsiques usant el càlcul de la derivada d'una funció. Els resultats s'amplien i, al final, es dóna un exemple amb una funció arbitrària.
Quadrat
 «
«
Es vol determinar la incertesa de
u(x) = x2
per a x = x0 ± δx. La derivada de la funció en el punt x0 indica les característiques de la funció:
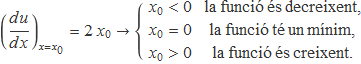
Per a un interval d'incertesa enfora de x = 0,
![]()
Per tant,
![]()
S'ha posat la derivada en valor absolut perquè l'expressió serveixi per a x0 negatiu. Per a x0 a prop de 0, s'ha de prendre
δu = Màxim[u(x0 – δx), u(x0 + δx)].
Arrel quadrada
 «
«
Es vol determinar la incertesa de
![]()
per a x = x0 ± δx amb x > 0. La derivada de la funció en el punt x0 és
![]()
Per tant,
![]()
Potència enèsima
 «
«
Es vol determinar la incertesa de
u(x) = xn,
per a x = x0 ± δx i n = 2, 3, 4, 5,... La derivada de la funció en el punt x0 indica les característiques de la funció:
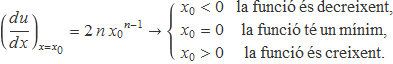
Per a un interval d'incertesa enfora de x = 0 on hi ha un mínim
![]()
Per tant,
![]()
S'ha posat la derivada en valor absolut perquè l'expressió serveixi per a x0 negatiu. Per a x0 a prop de 0, s'ha de prendre
δu = Màxim[u(x 0 – δx), u(x 0 + δx)].
Logaritme neperià
 «
«
Es vol determinar la incertesa de
u(x) = ln(x),
per a x = x0 ± δx amb x > 0. La derivada de la funció en el punt x0 és
![]()
Per tant,
![]()
Aquest resultat tan senzill és molt útil perquè indica que la incertesa relativa d'una variable x és igual a la incertesa absoluta de la variable u. El resultat es pot aprofitar per calcular la incertesa del producte i divisió de diferents variables.
Funció oscil·lant: Sinus cardinal
 «
«
Es vol determinar la incertesa de
![]()
per a x = x0 ± δx. La derivada de la funció en un punt x0 és
![]()
Per a un interval d'incertesa enfora dels extrems de la funció,
![]()
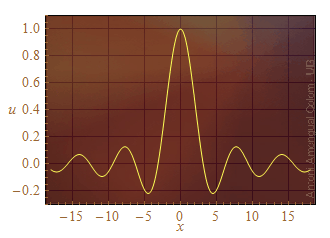
Figura 4. Gràfic de la funció sinus cardinal, sinc(x).
Una funció complicada prop de l'origen
 «
«
Conèixer la forma de la funció és important, especialment si la funció oscil·la ràpidament. La funció
![]()
es mostra a la Fig. 5. La funció oscil·la ràpidament prop de l'origen i la derivada de la funció pot donar problemes per avaluar la incertesa. Afortunadament, moltes de les funcions que s'han d'usar per fer càlculs amb les mesures del laboratori no tenen aquest comportament singular.

Figura 5. Gràfic d'una funció que oscil·la ràpidament (al passar el cursor sobre la imatge apareix una ampliació de la zona prop de l'origen).
El càlcul de la incertesa i la sèrie de Taylor
 «
«
El càlcul de la incertesa de la funció u(x) a partir de la incertesa de x es pot analitzar usant la sèrie de Taylor de la funció.
Cada un dels termes de la diferència
![]()
es calcularà usant la sèrie de Taylor de la funció al voltant del punt x0
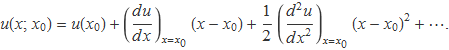
Per a x = x0 + δx es té
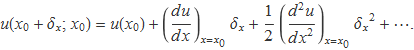
Per a x = x0 – δx es té
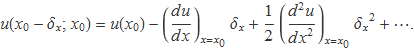
Els dos primers termes del desenvolupament donaran una bona aproximació si δx és petit i la derivada en el punt x0 és diferent de zero. Amb aquestes condicions es compleix,
![]()
Llavors,
![]()
Aquesta expressió es pot usar en els punts x0 on la funció sigui creixent o decreixent.
