
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Propagació de l'error
Discrepància
Definició «
Sigui x una magnitud física i siguin x1 ± δ1 i x2 ± δ2 dos resultats obtinguts a partir de mesures experimentals o càlculs teòrics.
La discrepància entre els dos valors és la diferència x2 – x1.
Es dirà que la discrepància és significativa si els intervals x1 ± δ1 i x2 ± δ2 no se solapen.
Quan les incerteses provenen d'errors aleatoris, els resultats seran del tipus x1 ± s1 i x2 ± s2 on s1 i s2 són desviacions estàndard. En aquests casos, la discrepància es dirà que és significativa si la diferència x2 – x1 és més gran que 2s1 o 2s2.
Exemple 1. Discrepen les mesures fetes per dos alumnes? «
En uns experiments per mesurar el coeficient de dilatació tèrmica d'un material, un alumne i la seva companya mesuren per separat la longitud d'una mateixa barra. Ell determina que la longitud és 1147 ± 3 mm i ella, 1149 ± 3 mm. Quina és la discrepància entre les mesures? És la discrepància significativa?
Resulta útil fer un gràfic com el de la Fig. 1 per visualitzar les barres d'error i els valors centrals.
La discrepància entre els dos valors mesurats pels alumnes val
Δ = 1149 – 1147 = 2 mm
i no és significant perquè els intervals d'incertesa se solapen.

Figura 1. Representació del valor i la incertesa de dues mesures.
Exemple 2. Podrien ser partícules diferents?
 «
«
Un grup d’investigació ha mesurat la massa d’una partícula i dóna com a resultat m1 = (7.8 ± 0.1) 10–27 kg. En una altra mesura, detecten una altra partícula de massa m2 = (7.0 ± 0.2) 10–27 kg. Es planteja si les dues mesures corresponen al mateix tipus de partícula. Per contestar, es determina la discrepància entre les dues mesures,
Δ = 0.8 10–27 kg.
Aquesta discrepància és significativa comparada amb la incertesa de les mesures com il·lustra la Fig. 2. Per tant, es podria tractar de partícules diferents.
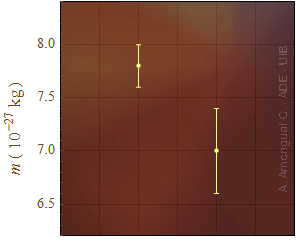
Figura 2. Representació del valor i la incertesa de dues mesures de la massa de partícules elementals.
Exemple 3. La mesura d'Arquímedes
 «
«

Figura 3. Quadre de Domenico Fetti (1620) imaginant com era Arquímedes de Siracusa (Siracusa, Sicilia, ca. 287 a. C. – ca. 212 a. C.).
La història d'Arquímedes cridant «Eureka», «ho he trobat», és molt coneguda. La relatà Marc Vitruvi Pol·lió (ca. 75 - 10 aC) en un dels seus llibres. Vitruvi relata que el tirà de Siracusa Hieró II lliurà una quantitat d'or a un orfebre perquè fes una corona a canvi d'un preu fixat per la feina. L'orfebre li tornà una corona molt ben feta que pesava el mateix que l'or que li havia estat lliurat. Hieró quedà satisfet amb la feina, però quan hi hagué una acusació que l'orfebre havia substituït part de l'or pel mateix pes de plata, Hieró demanà a Arquímedes si podia estudiar si l'havien enganat.
Arquímedes descobrí el mètode quan entrà dins una banyera i part de l'aigua vessà (llavors sortí suposadament pel carrer cridant «Eureka»).
En ficar peces d'or amb un pes igual al de la corona dins un recipient ple, part de l'aigua vessarà. Llavors, si es treuen les peces i es fica la corona dins el recipient, l'aigua arribarà fins la rima del recipient si la corona també és d'or; però si l'orfebre canvià part de l'or per plata, l'aigua vessarà en ficar la corona dins el recipient.
La idea d'Arquímedes es fonamenta en la diferència de densitat de l'or i la plata. El mètode funciona teòricament, però té limitacions que el poden fer inútil a la pràctica.
Considerem el problema numèricament suposant que la corona té 1 kg d'or, proper al valor típic d'una corona grega i que l'orfebre substitueix 200 grams d'or per 200 grams de plata. La diferència de volum entre una corona d'or i la que té plata és pot calcular usant les densitats dels dos metalls,
ρAu = 19300 kg / m3,
ρAg = 10490 kg / m3.
Les operacions que donen la diferència de volum són
![]()
Aquest canvi de volum es tradueix en un canvi d'altura del nivell de l'aigua del recipient on es fiqui la corona. Com que la corona no es podia espatllar ni deformar, cal suposar que el diàmetre de la boca del recipient hauria de tenir una mida d'uns 20 cm. Suposant que l'extrem fos cilíndric i tingués aquesta mida, el nivell de l'aigua que hauria de vessar seria de només
![]()
Aquesta diferència seria impossible de veure.
La mesura de la densitat del material de la corona i la de l'or permetrien resoldre el problema d'Hieró II. Naturalment, la discrepància entre el valor de la densitat de l'or i la densitat del material hauria de ser petita comparada amb la incertesa de la mesura. A la Fig. 4 es mostren dues mesures de la densitat del material del que està feta la corona. La mesura A permet concloure que la corona no és tota d'or. En canvi, la mesura B no permet establir una conclusió perquè la incertesa és massa gran.
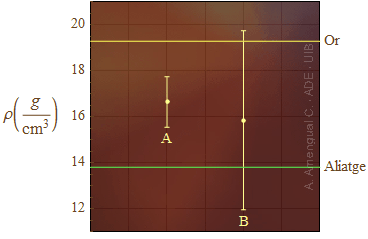
Figura 4. Representació del valor i la incertesa de dues mesures.
Per acabar, cal notar que el principi d'Arquímedes (que no s'aplica en el mètode descrit abans) es pot usar d'una manera simple per detectar si part del metall d'una peça s'ha canviat per un altre. La seqüència d'imatges següents ho explica.
1)
La figura representa dues peces del mateix volum i del mateix material penjades d'una barra suspesa pel centre. El pes de les dues peces és el mateix i la barra està horitzontal.
Figura 5. Aplicant el principi d'Arquímedes per resoldre el problema de la corona.
Exemple 4. Conservació del moment angular?
 «
«
En un experiment per comprovar el principi de conservació del moment angular, un estudiant mesura el moment angular d’un sistema en dos instants diferents. A la taula adjunta es mostren els resultats en kg m2/s de sis repeticions de la mesura. Quina és la incertesa de la diferència entre el moment angular a un temps i a un altre en cada mesura? Són aquests resultats consistents amb la conservació del moment angular?
| Inicial, J1 | Final, J2 |
| 3.0 ± 0.3 | 2.7 ± 0.6 |
| 7.4 ± 0.5 | 8 ± 1 |
| 14.3 ± 1.1 | 16.5 ± 1.2 |
| 25 ± 2 | 24 ± 2 |
| 32 ± 2 | 31 ± 2 |
| 37 ± 2 | 41 ± 2 |
Taula 1. Moments angulars en unitats SI d'un sistema en dos moments diferents i la diferència.
Per analitzar si les mesures són consistents amb la conservació del moment angular es pot procedir de tres maneres descrites a continuació.
És la resta consistent amb el valor 0?
 «
«
| Inicial, J1 | Final, J2 | J2 − J1 |
| 3.0 ± 0.3 | 2.7 ± 0.6 | -0.2 ± 0.9 |
| 7.4 ± 0.5 | 8 ± 1 | 0.6 ± 1.5 |
| 14.3 ± 1.1 | 16.5 ± 1.2 | 2.5 ± 2.5 |
| 25 ± 2 | 24 ± 2 | -1 ± 4 |
| 32 ± 2 | 31 ± 2 | -1 ± 4 |
| 37 ± 2 | 41 ± 2 | 4 ± 4 |
Taula 2. Moments angulars en unitats SI d'un sistema en dos moments diferents i la diferència.
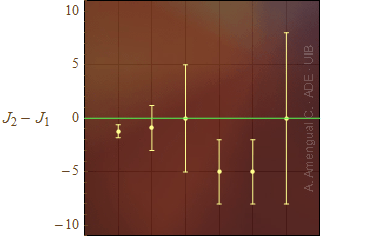
Figura 6. Representació del valor i la incertesa de la diferència entre el moment angular d'un sistema en dos moments diferents.
És la divisió consistent amb el valor 1?
 «
«
| Inicial, J1 | Final, J2 | J2 / J1 |
| 3.0 ± 0.3 | 2.7 ± 0.6 | 1.1 ± 0.4 |
| 7.4 ± 0.5 | 8 ± 1 | 0.92 ± 0.18 |
| 14.3 ± 1.1 | 16.5 ± 1.2 | 0.87 ± 0.13 |
| 25 ± 2 | 24 ± 2 | 1.04 ± 0.17 |
| 32 ± 2 | 31 ± 2 | 1.03 ± 0.13 |
| 37 ± 2 | 41 ± 2 | 0.90 ± 0.09 |
Taula 3. Moments angulars en unitats SI d'un sistema en dos moments diferents i el quocient.
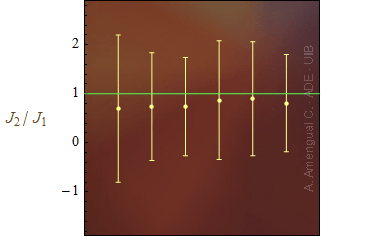
Figura 7. Representació del valor i la incertesa del quocient entre el moment angular d'un sistema en dos moments diferents.
Comprovació gràficament
 «
«
Per saber si les dades són consistents amb la conservació del moment angular J1 i J2 s'usaran com a valors de les coordenades d'un conjunt de punts i es comprovarà visualment si els punts estan sobre la recta J2 = J1.
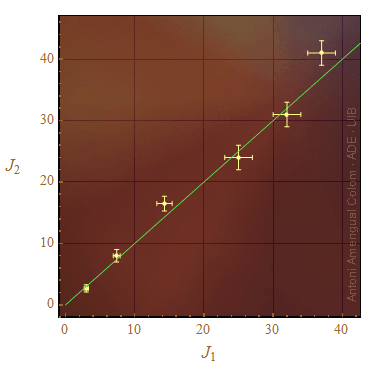
Figura 8. Representació dels valors de dues variables usats com a coordenades.
