La Fig. 1 es presentà en el tema sobre la propagació de la incertesa per funcions de n variables. El valor d'una magnitud es calculava amb una funció de quatre variables els valors de les quals s'havien determinat experimentalment i tenien determinades incerteses. Les quatre variables eren independents i la probabilitat que el valor real de totes elles fes augmentar el valor de la magnitud calculada havia de ser més petita que la probabilitat que almenys alguna els fes minvar.

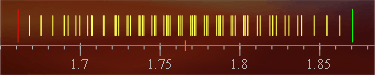
Figura 1. Aquesta figura es presentà en un tema anterior a l'apartat «Exemple amb la mesura de la relació u = e/m».

Quan es dóna un resultat en la forma x = x₀ ± δ_x s'ha de saber quin tipus d'error és δ_x perquè la interpretació del resultat canvia. En alguns casos, δ_x pot ser una cota absoluta dels valors de x. En tal cas, s'està segur que el valor de x està dins l'interval [x₀ – δ_x, x₀ + δ_x]. Però amb errors aleatoris, δ_x és habitualment l'error estàndard s_x (tal vegada corregit pel factor de Student). En tal cas, només s'està segur que el resultat estarà dins l'interval [x₀ – δ_x, x₀ + δ_x] amb una probabilitat del 68%.

Fer una mesura d'una magnitud en presència de diverses fonts d'errors aleatoris és com mirar el valor que pren a l'atzar una variable aleatòria gaussiana. La mitjana i la variància de la funció densitat de probabilitat d'aquesta variable són desconegudes, però es poden estimar amb la mitjana i l'error estàndard d'un conjunt de mesures de la magnitud considerada.

Amb errors aleatoris, escriure x₁ = m₁ ± s₁ és com dir que hi ha una funció densitat de probabilitat gaussiana G_μ,σ(x) de mitjana μ = m₁ i desviació estàndard s₁ que es pot usar per determinar la probabilitat que el valor real de x estigui dins un determinat interval.

La mateixa interpretació es pot fer per a una altra magnitud x₂ = m₂ ± s₂. Llavors resulta immediat plantejar la qüestió de quina funció densitat de probabilitat tendran les magnituds calculades a partir de x₁ i x₂. Les operacions bàsiques considerades explícitament en aquest bloc de temes seran multiplicar una magnitud per una constant (c x₁), sumar dues magnituds (x₁ + x₂) i dividir-les (x₁ / x₂). En general, s'usaran funcions d'una variable u(x₁) o de dues, v(x₁, x₂).

Els casos c x₁ i x₁ + x₂ tenen una transcendència més gran de la que pot semblar atesa la simplicitat de les expressions. Si la funció densitat de probabilitat de les variables són gaussianes, G_μ1,s1(x) i G_μ2,s2(x),  la funció densitat de probabilitat dels valors c x₁ també és gaussiana, amb mitjana c μ₁ i variància c σ₁. La funció densitat de probabilitat dels valors x₁ + x₂ es dóna a la Taula 1. Els resultats d'aquests dos casos són el punt de partida per analitzar valors calculats amb funcions d'una, dues o més variables.

Quan les incerteses són petites, les funcions es poden aproximar per sèries de Taylor de primer ordre. Així, els valors de les funcions es poden calcular amb expressions dels tipus

u(x₁, x₂) = c₀ + c₁ x₁ + c₂ x₂,

on c₀ és una constant (que no canvia la variància) i c₁ i c₂ són les derivades parcials de la funció avaluades a x₁ = μ₁ i x₂ = μ₂. La multiplicació per una constant o la suma amb altres variables gaussianes no canvia el fet que la funció densitat de probabilitat dels valors obtinguts sigui gaussiana. La Taula 1, recull les expressions de les mitjanes i la variàncies que es demostraran en els temes següents d'aquest bloc. En el darrer tema, la funció densitat de probabilitat dels valors x₁ / x₂, que es pot calcular de manera exacta de manera no massa difícil, es compararà amb la gaussiana calculada de manera aproximada desenvolupant x₁ / x₂ en sèrie de Taylor a primer ordre.

Taula 1. Relació de les mitjanes i variàncies de les variables indicades amb les mitjanes i variàncies de les variables x₁ i x₂. El subíndex μ a les derivades indica que s'han d'avaluar a x₁ = μ₁, x₂ = μ₂.