
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM ![]() -2013.
-2013.
Distribució normal (gaussiana)
Integral de la funció densitat de probabilitat
Introducció  «
«
Es presenta la integral de la funció densitat de probabilitat gaussiana

i la taula de valors d'aquesta integral. Els fulls de càlcul i altres programes informàtics tenen funcions per calcular la integral per a qualsevol valor de x0. Les taules es presenten per plantejar l'exercici de trobar la incertesa d'un valor obtingut per interpolació.
La integral en un interval finit a partir de la integral des de menys infinit a x0  «
«
La probabilitat que una variable aleatòria x amb funció de distribució de probabilitat gaussiana prengui un valor dins l'interval [xmin, xmàx] és
![]()
amb la funció
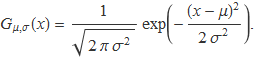
Si es té present que una integral dóna l'àrea sota la corba, resultarà obvi que la integral que dóna la probabilitat P es pot calcula amb la resta (Fig. 1)
![]()
Aquesta separació revela la utilitat de definir la funció integral Iμ,σ de la funció gaussiana:
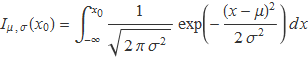
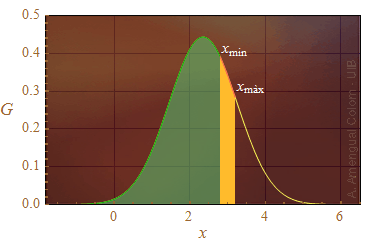
Figura 1. L'àrea de la zona taronja dóna la probabilitat d'obtenir x entre xmin i xmàx.
Les funcions trigonomètriques d'un angle o el logaritme d'un número es consultaven en taules fins que les calculadores les feren innecessàries.
El valor de la integral Iμ,σ es pot obtenir amb un full de càlcul. La instrucció per a excel o calc és DISTR.NORM(x0; μ; σ; c) amb c = 1 (cert). La funció dóna el valor de la gaussiana en lloc de la integral si es posa c = 0.
No és l'ús de la taula el que resulta interessant aquí sinó els exercicis que es resoldran usant-la.
Relació amb la integral de la gaussiana centrada a l'origen i variància unitat  «
«
Les integrals d'una funció gaussiana es poden relacionar amb la integral de la gaussiana centrada a l'origen i amb desviació estàndard unitat, G0,1(x), amb el canvi de variable
![]()
Es tendrà dx = σ dz i el límit superior de la integral passarà a ser
![]()
de manera que
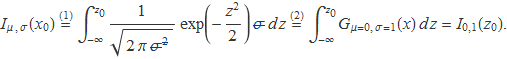
En el pas (1) s'ha fet el canvi de variable i, en el pas (2), s'ha identificat la funció amb la gaussiana de mitjana 0 i variància 1. Resulta així que
![]()
i, en conseqüència, coneixent
![]()
es podran calcular les probabilitats per a tot tipus de gaussianes. Els valors d'aquesta integral per a un conjunt de valors z0 = a + b es donen a la taula presentada a l'apartat següent.
Taula dels valors de la integral de la gaussiana de mitjana 0 i variància unitat  «
«
A la Taula 1 es presenten els valors de la integral
![]()
Només s'inclouen valors de z0 = a + b positius perquè la gaussiana és simètrica i està normalitzada, de manera que
![]()
Aquesta relació s'il·lustra a la Fig. 2 i es basa en que l'obtenció de z > z0 és el succés complementari d'obtenir z ≤ z0.
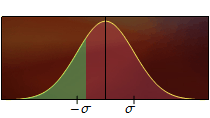
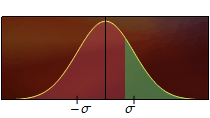
Figura 2. L'àrea total sota la corba és 1, de manera que l'àrea verda de l'esquerra és igual a 1 menys l'àrea vermella de la dreta la qual s'obté amb la funció I(z).
| a\b | 0. | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.0 | 0.50000 | 0.50399 | 0.50798 | 0.51197 | 0.51595 | 0.51994 | 0.52392 | 0.52790 | 0.53188 | 0.53586 |
| 0.1 | 0.53983 | 0.54380 | 0.54776 | 0.55172 | 0.55567 | 0.55962 | 0.56356 | 0.56749 | 0.57142 | 0.57535 |
| 0.2 | 0.57926 | 0.58317 | 0.58706 | 0.59095 | 0.59483 | 0.59871 | 0.60257 | 0.60642 | 0.61026 | 0.61409 |
| 0.3 | 0.61791 | 0.62172 | 0.62552 | 0.62930 | 0.63307 | 0.63683 | 0.64058 | 0.64431 | 0.64803 | 0.65173 |
| 0.4 | 0.65542 | 0.65910 | 0.66276 | 0.66640 | 0.67003 | 0.67364 | 0.67724 | 0.68082 | 0.68439 | 0.68793 |
| 0.5 | 0.69146 | 0.69497 | 0.69847 | 0.70194 | 0.70540 | 0.70884 | 0.71226 | 0.71566 | 0.71904 | 0.72240 |
| 0.6 | 0.72575 | 0.72907 | 0.73237 | 0.73565 | 0.73891 | 0.74215 | 0.74537 | 0.74857 | 0.75175 | 0.75490 |
| 0.7 | 0.75804 | 0.76115 | 0.76424 | 0.76730 | 0.77035 | 0.77337 | 0.77637 | 0.77935 | 0.78230 | 0.78524 |
| 0.8 | 0.78814 | 0.79103 | 0.79389 | 0.79673 | 0.79955 | 0.80234 | 0.80511 | 0.80785 | 0.81057 | 0.81327 |
| 0.9 | 0.81594 | 0.81859 | 0.82121 | 0.82381 | 0.82639 | 0.82894 | 0.83147 | 0.83398 | 0.83646 | 0.83891 |
| 1.0 | 0.84134 | 0.84375 | 0.84614 | 0.84849 | 0.85083 | 0.85314 | 0.85543 | 0.85769 | 0.85993 | 0.86214 |
| 1.1 | 0.86433 | 0.86650 | 0.86864 | 0.87076 | 0.87286 | 0.87493 | 0.87698 | 0.87900 | 0.88100 | 0.88298 |
| 1.2 | 0.88493 | 0.88686 | 0.88877 | 0.89065 | 0.89251 | 0.89435 | 0.89617 | 0.89796 | 0.89973 | 0.90147 |
| 1.3 | 0.90320 | 0.90490 | 0.90658 | 0.90824 | 0.90988 | 0.91149 | 0.91309 | 0.91466 | 0.91621 | 0.91774 |
| 1.4 | 0.91924 | 0.92073 | 0.92220 | 0.92364 | 0.92507 | 0.92647 | 0.92785 | 0.92922 | 0.93056 | 0.93189 |
| 1.5 | 0.93319 | 0.93448 | 0.93574 | 0.93699 | 0.93822 | 0.93943 | 0.94062 | 0.94179 | 0.94295 | 0.94408 |
| 1.6 | 0.94520 | 0.94630 | 0.94738 | 0.94845 | 0.94950 | 0.95053 | 0.95154 | 0.95254 | 0.95352 | 0.95449 |
| 1.7 | 0.95543 | 0.95637 | 0.95728 | 0.95818 | 0.95907 | 0.95994 | 0.96080 | 0.96164 | 0.96246 | 0.96327 |
| 1.8 | 0.96407 | 0.96485 | 0.96562 | 0.96638 | 0.96712 | 0.96784 | 0.96856 | 0.96926 | 0.96995 | 0.97062 |
| 1.9 | 0.97128 | 0.97193 | 0.97257 | 0.97320 | 0.97381 | 0.97441 | 0.97500 | 0.97558 | 0.97615 | 0.97670 |
| 2.0 | 0.97725 | 0.97778 | 0.97831 | 0.97882 | 0.97932 | 0.97982 | 0.98030 | 0.98077 | 0.98124 | 0.98169 |
| 2.1 | 0.98214 | 0.98257 | 0.98300 | 0.98341 | 0.98382 | 0.98422 | 0.98461 | 0.98500 | 0.98537 | 0.98574 |
| 2.2 | 0.98610 | 0.98645 | 0.98679 | 0.98713 | 0.98745 | 0.98778 | 0.98809 | 0.98840 | 0.98870 | 0.98899 |
| 2.3 | 0.98928 | 0.98956 | 0.98983 | 0.99010 | 0.99036 | 0.99061 | 0.99086 | 0.99111 | 0.99134 | 0.99158 |
| 2.4 | 0.99180 | 0.99202 | 0.99224 | 0.99245 | 0.99266 | 0.99286 | 0.99305 | 0.99324 | 0.99343 | 0.99361 |
| 2.5 | 0.99379 | 0.99396 | 0.99413 | 0.99430 | 0.99446 | 0.99461 | 0.99477 | 0.99492 | 0.99506 | 0.99520 |
| 2.6 | 0.99534 | 0.99547 | 0.99560 | 0.99573 | 0.99585 | 0.99598 | 0.99609 | 0.99621 | 0.99632 | 0.99643 |
| 2.7 | 0.99653 | 0.99664 | 0.99674 | 0.99683 | 0.99693 | 0.99702 | 0.99711 | 0.99720 | 0.99728 | 0.99736 |
| 2.8 | 0.99744 | 0.99752 | 0.99760 | 0.99767 | 0.99774 | 0.99781 | 0.99788 | 0.99795 | 0.99801 | 0.99807 |
| 2.9 | 0.99813 | 0.99819 | 0.99825 | 0.99831 | 0.99836 | 0.99841 | 0.99846 | 0.99851 | 0.99856 | 0.99861 |
Taula 1. Àrea sota la corba de la funció de distribució gaussiana de mitjana 0 i desviació estàndard 1 des de menys infinit fins a a + b.
Valors que s'haurien de recordar  «
«
A la Fig. 3 es mostren sis àrees els valors de les quals s'haurien de recordar.
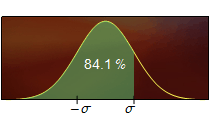
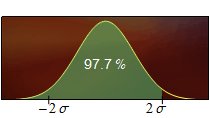
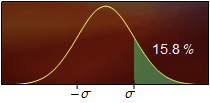

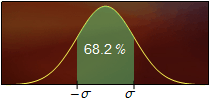
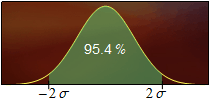
Figura 3. L'àrea destacada en color verd representa el percentatge indicat de l'àrea total.
Exemples  «
«
Es consideren a continuació tres casos típics que s'han de saber resoldre.
Ús directe de la taula  «
«
La probabilitat que un succés aleatori amb probabilitat gaussiana de mitjana 0 i variància 1 doni un valor inferior a a+ b, amb
a = 0.7,
b = 0.02,
es pot obtenir directament de la taula amb cinc decimals,
![]()
| a\b | 0. | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.6 | 0.72575 | 0.72907 | 0.73237 | 0.73565 | 0.73891 | 0.74215 | 0.74537 | 0.74857 | 0.75175 | 0.75490 |
| 0.7 | 0.75804 | 0.76115 | 0.76424 | 0.76730 | 0.77035 | 0.77337 | 0.77637 | 0.77935 | 0.78230 | 0.78524 |
| 0.8 | 0.78814 | 0.79103 | 0.79389 | 0.79673 | 0.79955 | 0.80234 | 0.80511 | 0.80785 | 0.81057 | 0.81327 |
Taula 2. Valor de la taula corresponent a a + b = 0.72 destacat en vermell.
Càlcul per interpolació  «
«
La probabilitat que un succés aleatori amb probabilitat gaussiana de mitjana 0 i variància 1 doni un valor més petit que un valor donat amb més dos decimals, s'ha de calcular interpolant entre dos valors de la taula.
En general, si x1 < x < x2 s'usarà
![]()
Per exemple, I0,1(0.724) es determinarà mirant els valors de I0,1(0.72) i I0,1(0.73) i suposant que hi ha una variació lineal del valor de la integral (Fig. 3)
![]()
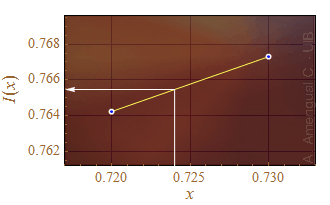
Figura 4. Donat el valor de la integral per a dues abscisses, el valor en un punt intermedi es pot determinar aproximadament suposant que I(x) varia linealment.
Incertesa del valor interpolat  «
«
Els valors de la integral I0,1(x) de la taula estan arrodonits al cinquè decimal. El valor exacte sense arrodonir és el de la taula més o menys 0.000005.
L'arrodoniment a un nombre finit de decimals introdueix incertesa. El valor exacte podria ser qualsevol que arrodonit a cinc decimals donés el que surt. Sense més informació disponible, s'ha de suposar que
![]()
Usant els valors 0.764235 i 0.767305, la interpolació dóna 0.765465. Però els valors extrems es poden combinar de quatre maneres i es donen quatre possibles valors de la interpolació. Els valors mínim i màxims són 0.765459 i 0.765469. El valor central és
![]()
Com que el màxim i el mínim disten d'aquest valor central
![]()
el resultat es pot expressar en la forma
![]()
El valor exacte amb sis decimals és 0.765467. La diferència amb el valor central és 0.000003 < 0.000005.
En general es pot cercar la incertesa sobre la integral usant les fórmules de la propagació de l'error per la funció
![]()
Per simplificar la notació, s'escriurà
![]()
Es tendrà
![]()
Es calcularà ara només l'error degut als dos primers termes
![]()
Com que x està entre x1 i x2 es poden llevar els valors absoluts i, com que les incerteses sobre I1 i I2 són iguals, només queda
![]()
Integral d'una gaussiana de mitjana i desviació estàndard qualsevol  «
«
La probabilitat que en un succés aleatori amb probabilitat gaussiana de mitjana μ i variància σ s'obtengui un valor x0 s'ha de determinar amb la taula usant la relació
![]()
Per calcular la probabilitat d'obtenir x < 5.04 amb la funció densitat de probabilitat gaussiana de mitjana 4.8 i desviació estàndard 1/3, primer s'ha de fer el canvi de variable
![]()
En general el valor de z0 no sortirà a la taula i s'haurà de fer una interpolació; però, en aquest cas, es pot usar la taula directament per obtenir
![]()
La igualtat entre els dos primers termes està il·lustrada a la Fig. 4.
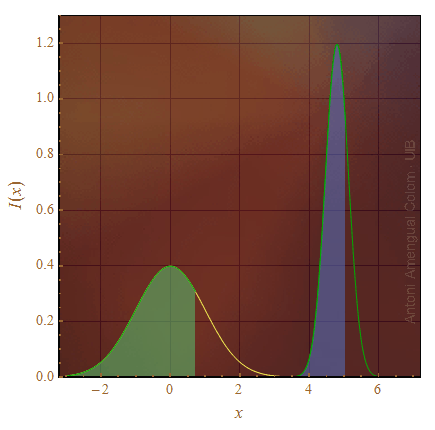
Figura 5. L'àrea sota una gaussiana es pot relacionar amb l'àrea sota una gaussiana centrada en l'origen i de desviació estàndard unitat fent un canvi de variable. L'àrea de la zona blava de la figura és igual a l'àrea de la zona verda.

