Es demostrarà en aquest tema que la funció densitat de probabilitat d'una variable aleatòria suma de dues variables aleatòries gaussianes també és gaussiana. La mitjana i la variància són iguals a les sumes de les mitjanes i de les variàncies, respectivament.

Siguin X₁ i X₂ dues variables aleatòries gaussianes amb funcions densitat de probabilitat

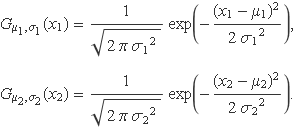
Cercam la funció densitat de probabilitat de la variable aleatòria X els valors de la qual són la suma d'un valor de la variable X₁ i un valor de la variable X₂,

x = x₁ + x₂.

Un valor x = x₀ es pot obtenir d'infinites maneres. Per a tot valor de x₁, el valor x₂ = x₀ – x₁ dóna la suma x₀. Per tant, la funció densitat de probabilitat per a x = x₀ és

Aquesta expressió és formalment com la que s'escrigué per a la funció densitat de probabilitat de la suma de nos números aleatoris generats amb una calculadora.

Usant l'expressió de les gaussianes, es té

on

Els exponents es poden sumar i escriure

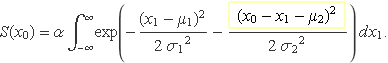
El terme dins el requadre groc es compararà amb un terme que sortirà en analitzar la resta de dues variables aleatòries en el pròxim apartat. El valor de α no és rellevant perquè la funció de probabilitat s'ha de normalitzar.

Usant taules d'integració es troba que

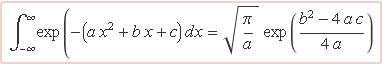
La integral que dóna S(x₀) es pot escriure d'aquesta manera. Desenvolupant els termes i identificant el terme independent i els coeficients que multipliquen a x i a x², es troba

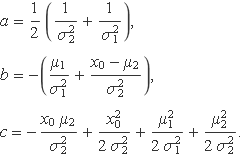
Després de nombroses operacions resulta

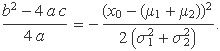
Per tant,

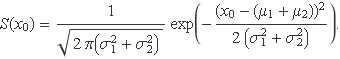
Aquest resultat indica que la variable aleatòria suma també té una funció densitat de probabilitat gaussiana, la mitjana i la variància de la qual són:

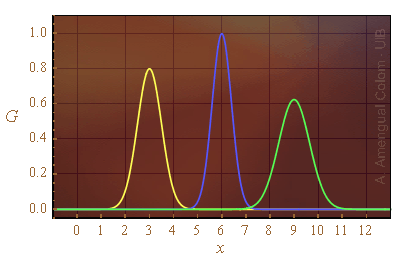
Figura 1. La línia verda és la funció densitat de probabilitat gaussiana de la suma de la variable aleatòria amb la funció densitat de probabilitat gaussiana de color groc més la de color blau.

Per a la resta de variables aleatòries gaussianes,

x = x₁ − x₂.

es podria repetir el càlcul que s'ha fet a l'apartat anterior considerant que un valor x = x₀ es pot obtenir d'infinites maneres perquè per a tot valor de x₁, el valor x₂ = x₁ – x₀ dóna per a la resta x = x₀. Per tant, la probabilitat de tenir x₀ és

Usant les expressions de les gaussianes i unint els exponents quedarà

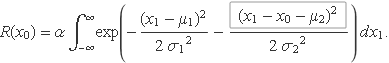
La constant α s'ha definit a l'apartat anterior. El terme que s'ha escrit dins el requadre gris està al quadrat i el signe de tots els termes dins els parèntesis es pot canviar sense alterar el resultat; llavors, els termes es poden reordenar:

D'aquesta manera s'obté el mateix terme del requadre groc de l'expressió de S(x₀) excepte perquè el signe de μ₂ ha canviat. Però μ₂ és un paràmetre que no intervé en la integració i el resultat de la integral serà al mateix de l'apartat anterior canviant el signe de μ₂. Així,

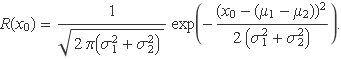
Aquest resultat indica que la variable aleatòria resta també té una funció densitat de probabilitat normal, la mitjana i la variància de la qual són:

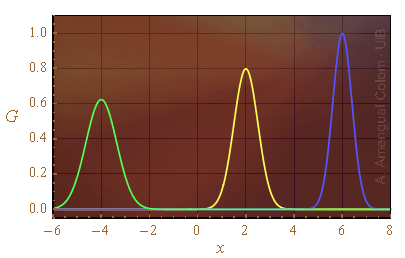
Figura 2. La línia verda és la funció densitat de probabilitat gaussiana de la resta de la variable aleatòria amb la funció densitat de probabilitat gaussiana de color groc menys la de color blau.