Es determinarà la funció densitat de probabilitat de la suma de dos números aleatoris obtinguts amb una calculadora (tecla RAN#) i es mostrarà la funció densitat de probabilitat de la suma de tres números.

La tecla RAN# d'una calculadora genera números aleatoris de tres decimals homogèniament dins l’interval [0, 1]. La funció de probabilitat té valors per a n/1000 on n és ún número de l'interval [0, 999]. La funció és constant i pren el valor 0.001 perquè la probabilitat que surti un valor concret és igual a un cas favorable entre mil possibles.

Si es disposés d'un generador de números reals homogèniament entre 0 i 1, s'hauria de parlar de la funció densitat de probabilitat P(x). La funció es mostra a la Fig. 1. És constant i val 1 dins el domini [0, 1].

L'escala vertical d'una funció densitat de probabilitat es pot determinar considerant que la integral de la funció sobre el domini o univers Ω ha de valer 1.

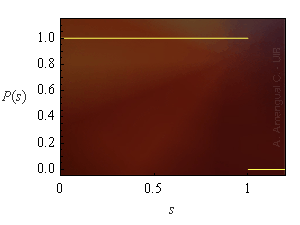
Figura 1. La funció de probabilitat del números aleatoris generats amb la calculadora és constant dins l'interval (0, 1) i nul·la fora.

Amb un generador de números reals x (o simplement amb més de tres decimals) es podrien arrodonir els valors obtinguts a tres decimals. La probabilitat d'obtenir r = n/1000, és la probabilitat que x estigui a una distància de 0.0005 unitats de r. Així,  

Naturalment la probabilitat torna ser 0.001.

Les calculadores i els ordenadors sempre donen un nombre finit de decimals. No obstant això, es útil considerar que es pot usar una funció densitat de probabilitat i, com s'ha mostrat ara, s'obtenen resultat coherents. L'univers dels números aleatoris que s'obtenen al sumar RAN# + RAN# és de 1999 valors entre 0 i 1.998. En lloc de calcular la funció de probabilitat per aquest conjunt discret de valors, es calcularà la funció densitat de probabilitat suposant que RAN# genera números aleatoris reals.

Considerem dues urnes opaques que contenen bolles numerades, de l'1 al 5 la primera i del 7 al 10 la segona.

Quina és la probabilitat d'extreure una bolla de cada urna i que la suma dels números sigui dotze?

La resposta es pot calcular de dues maneres. Hi ha 5 números dins una urna i 4 dins l'altra. En total hi ha vint casos, dels quals, quatre donen dotze: 2 + 10, 3 + 9, 4 + 8 i 5 + 7. La regla de Laplace dóna    

Una altra manera de calcular la resposta és sumar la probabilitat dels quatre casos que donen dotze. La frase «que surti 2 i 10, o 3 i 9, o 4 i 8, o 5 i 7» dóna

que és 1/5 perquè P_v(x) = 1/5 per a totes les bolles vermelles i P_b(x) = 1/4 per a totes les blaves.

La darrera expressió es pot posar en la forma general, per a qualsevol suma:

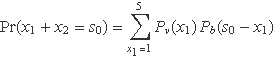
assumint que P_b(r) és 0 si r no és 7, 8, 9 o 10.

Quan es pitja dues vegades la tecla RAN# i s'obtenen dos números de tres decimals, és com si s'extraguessin dues bolles d'urnes amb mil bolles cada una. El sumatori tendria ara mil termes.

Si els valors aleatoris que s'han de sumar fossin dos números reals, s'hauria de demanar la probabilitat que la suma estés dins l'interval [ s₀, s₀ + δ_s ] i s'hauria de calcular

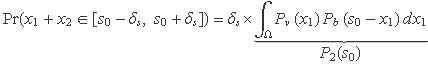
La integració s'ha de fer sobre el domini Ω de x₁, és equivalent a la suma del cas discret i defineix P₂(s₀), on el subíndex 2 recorda que és la funció densitat de probabilitat de la suma de dos números aleatoris. Si es generen dos números aleatoris amb la mateix funció densitat de probabilitat, es pot prescindir dels subíndex v i b. A més, si Ω ∈ [0, 1], es tendrà

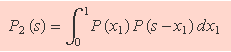
A continuació es determinarà aquesta funció.

La suma de dos números aleatoris entre 0 i 1, s = x₁ + x₂, serà un número entre 0 i 2. La densitat de probabilitat en aquest interval serà, com s'ha avançat a l'apartat anterior,

Per calcular aquesta integral, s'ha de tenir present que

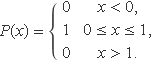
A continuació, quan s'hagi de calcular P(s – x₁) s'ha de considerar que valdrà 1 si s – x₁ té un valor dins l'interval [0, 1] i 0 en cas contrari.

Dins l'interval d'integració [0, 1], P(x₁) = 1 i només queda un terme dins la integral,

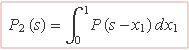
Per fer la integració convé distingir si s és més petit o més gran que 1.

La integral de P₂(s) per a s ∈ [0, 1] se separa en dues dividint el domini d'integració en dues parts, de 0 a s i de s a 1,

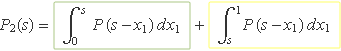
La primera integral es fa per a x₁ ∈ [0, s], per tant s – x₁ ∈ [0, s] amb 0 ≤ s ≤ 1, de manera que P(s – x₁) = 1. Llavors la primera integral dóna

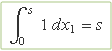
La segona integral es fa per a x₁ ∈ [s, 1], per tant s – x₁ sempre és negatiu i l'integrand P(s – x₁) serà zero. La segona integral és nul·la:

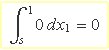
Usant els resultats de les dues integrals s'obté

La integral de P₂(s) per a s ∈ [1, 2] es calcula fent el canvi de variable z = s – x₁:

El límit superior de la integral es pot substituir per 1 perquè la densitat de probabilitat per a z > 1 és zero. Deixant només l'interval on la densitat val 1, es té

Reunint els resultats dels dos apartats anteriors, la funció densitat de probabilitat de la suma de dos números aleatoris entre 0 i 1 és

El gràfic de la funció es mostra a la Fig. 2.

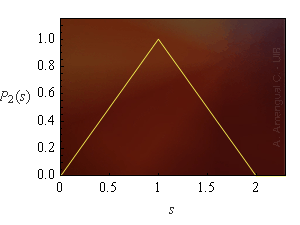
Figura 2. La funció densitat de probabilitat de la suma de dos números aleatoris generats amb la calculadora.

La densitat de probabilitat per a la variable aleatòria suma s = x₁ + x₂ + x₃ és

La realització de la integració és laboriosa i només es mostra el resultat a la Fig. 3 (línia groga). A la figura s'ha dibuixat la funció gaussiana que té la mateixa mitjana i variància (σ = 0.25) amb una línia verda. La diferència entre les dues funcions és petita i es podria comprovar que P_n(x) se sembla cada vegada més a una gaussiana quan n augmenta.

Figura 3. La funció densitat de probabilitat de la suma de tres números aleatoris generats amb la calculadora (línia groga) i la funció gaussiana de la mateixa mitjana i variància.

En aquest apartat se generen números aleatoris entre 0 i 1 i les sumes de dos o tres d'ells. Els números no es mostren però s'agrupen per donar una funció de probabilitat que es presenta en forma d'histograma amb escala vertical arbitrària (si es vol, es poden veure els valors pitjant el botó [valors]). L'interval [0, S] on S serà 1, 2 o 3 segons el nombre de números aleatoris que se sumen, es divideix en cert nombre d'intervals (73 a l'exemple). L'amplada de cada interval és S/73. En el cas S = 2, el primer interval és [0, 2/73] i sempre que la suma de dos números aleatoris doni dins aquest interval, se sumarà una unitat a la primera barra de l'histograma. La probabilitat d'obtenir un número aleatori dins un determinat interval es pot calcular a partir de l'àrea sota la funció densitat de probabilitat. Per exemple, la probabilitat que la suma doni entre uns valors a i b donats, ambdós més petits que 1, és fàcil de calcular perquè és la d'un trapezi:

Si es generen N sumes, s'espera un nombre de l'ordre de N×(b+a)(b–a)/2 estiguin dins l'interval [a, b]. Aquestes línies han de servir per donar una idea de la forma de l'histograma que cal esperar: una forma escalonada simètrica.

Es pot comprovar amb l'aplicació segúent que les funcions de probabilitat s'acosten a les formes de les funcions densitat de probabilitat de les Figs. 1, 2 i 3 quan el nombre de dades generat és gran.

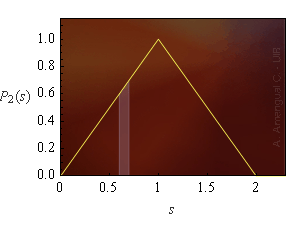
Figura 4. L'àrea marcada dóna la probabilitat que la suma de dos números aleatoris entre 0 i 1 doni un valor dins l'interval de la base d'aquesta àrea.

Descripció de les funcions dels botons »

L'histograma mostrat a partir d'un cert nombre de dades es reescala per mantenir l'altura dins el quadre del dibuix.