
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Distribució normal (gaussiana)
Definició de la funció gaussiana
Definició i gràfic «
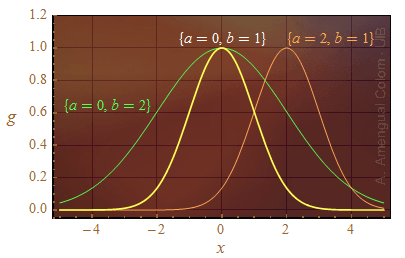
Figura 1. La funció gaussiana per a tres parelles de valors dels paràmetres que la defineixen.
La funció de la variable x
![]()
amb a i b dos números reals, s'anomena funció gaussiana. La forma d'aquesta funció per a tres parelles de valors dels paràmetres a i b es mostra a la Fig. 1. El paràmetre a determina on hi ha el màxim i el paràmetre b, la rapidesa amb que la funció tendeix a zero quan x s'allunya del màxim.
En el denominador de l'exponent es podria posar una constant simple però es posa una constant b al quadrat per deixar clar que l'exponent sempre serà negatiu, i es multiplica per 2 perquè els punts d'inflexió que té la funció quedin a x = a ± b.
Característiques bàsiques
 «
«
Es presenten a continuació quatre característiques bàsiques de la funció gaussiana.
Màxim
 «
«
L'equació de la primera derivada igualada a zero es resol fàcilment:
![]()
El valor màxim és g(a) = 1.
Punts d'inflexió
 «
«
La funció gaussiana té punts d'inflexió a una distància b a cada costat del màxim.
La segona derivada igualada a zero s'anula a les arrels d'una equació de segon grau. Les arrels són
![]()
El valor de la funció en els punts d'inflexió és
g(a ± b) = exp(–0.5) = 0.607.
Simetria
 «
«
La funció gaussiana és simètrica respecte al màxim.
La funció depèn de (x – a)2 que pren valors iguals per a valors de x equidistants de a, llavors
g(a – d) = g(a + d)
per a tot valor d.
Límits
 «
«
Per a x → –∞ i x → –∞ l'exponent tendeix a –∞ i l'exponencial a zero.
