Un histograma és «una representació gràfica d'una distribució de freqüències per mitjà de rectangles, les amplàries dels quals representen intervals de la classificació i les altures de la qual representen les corresponents freqüències».^‡ També es dibuixen histogrames on les altures dels rectangles són proporcionals al nombre de casos en lloc de ser-ho a les freqüències. Addicionalment, el rectangle és la figura genèrica, però es poden usar altres formes i convé usar un punt en el centre del costat superior del rectangle en lloc del propi rectangle quan hi ha molts d'intervals de classificació (classes), com a la Fig. 4 o a la Fig. 7.

L'histograma resulta útil per visualitzar la forma de la funció de probabilitat d'una variable aleatòria discreta. També serveix per visualitzar la forma de la funció densitat de probabilitat d'una variable aleatòria continua agrupant diversos valors de la variable per construir l'histograma.

Quan l'histograma s'usi per representar freqüències o valors d'una variable discreta obtinguts experimentalment, serà necessari agrupar diverses classes si el nombre de valors que pot prendre la variable és gran comparat amb el nombre n de resultats disponibles. En aquestes circumstàncies, les freqüències només prendrien els valors 1/n o 0 si no es fes l'agrupació. Si la variable és continua, s'ha de fer una agrupació per intervals adient.

El temps de carrera es mesura en segons en les proves de marató. Paula Radcliffe és la dona que fins ara ha completat una prova de marató més aviat. Radcliffe completà la marató de Londres de 2003 en 2 h 15 min 25 s. Els temps de les participants en una marató multitudinària queden repartits per damunt d'aquest temps (excepte per un eventual nou rècord), però moltes participants arriben a la meta totes soles, de manera que hi ha molts de temps que ningú no ha fet i molts de temps que ha fet només una corredora. El temps de carrera és una variable discreta però hi ha més valors possibles que participants i, si no s'agrupen, l'histograma tendrà moltes zones formades per rectangles aïllats, corresponents a una única participant, entre zeros. L'agrupació dels valors en intervals de dos minuts permet tenir un nombre adient de corredores a cada interval. A la Fig. 1 es mostra l'histograma dels temps de les participants a la marató d'Estocolm de 2012. La forma de campana indica que els temps es podrien modelar amb la funció gaussiana.

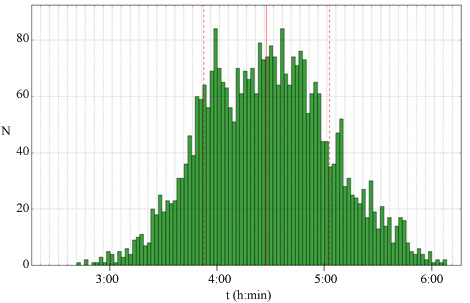
Figura 1. Histograma del temps emprats per les 3343 dones que corregueren la marató d'Estocolm del 2 de juny de 2012 agrupades per intervals de 2 minuts (font: anderswallin.net). En l'eix vertical es dóna el número de dones i no el número dividit pel total de participants.

La funció densitat de probabilitat del mòdul de la velocitat de les molècules d'un gas a temperatura absoluta T que calcularen J. C. Maxwell i L. Boltzmann és

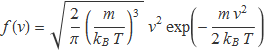
on m és la massa de les molècules i k_B és la constant de Boltzmann. La Fig. 3 mostra l'histograma agrupant la densitat de probabilitat de les velocitats moleculars en intervals de 0.2 vegades la velocitat més probable.

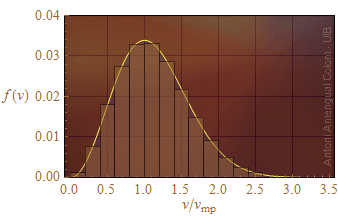
Figura 2. Densitat de probabilitat del mòdul de la velocitat de les molècules d'un gas amb l'histograma esperat agrupant les velocitat per intervals finits.

L'histograma teòric mai es reproduirà igual al construir-se amb dades experimentals. Es té l'histograma de la població (l'esperat) i l'histograma d'una mostra. En alguns casos es coneix exactament quin és l'histograma de la població i en altres es fa una hipòtesi de treball, considerant que es pot aplicar una determinada distribució de probabilitat. A continuació es comenten alguns exemples.

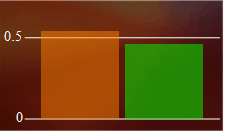
Figura 3. Freqüència de cares (columna taronja) i creus (verda) després de llançar 50 vegades una moneda.

La probabilitat d'obtenir cara o creu en el llançament d'una moneda sense trucar és 0.5 en cada cas, però l'histograma construït llançant la moneda un cert nombre de vegades no mostrarà aquesta igualtat. No obstant això, la diferència no indica que la distribució de probabilitat esperada no sigui correcta o que la moneda estigui trucada. La desigualtat només podrà considerar-se significativa si sorgeix de molts de llançaments i és més gran que un determinat valor.

Els punts verds de la figura següent corresponen a la freqüència amb la qual han sortit n_c cares quan s'han fet mil llançaments simulats d'una moneda. Aquesta freqüència s'ha obtingut simulant 10000 repeticions dels mil llançaments. La línia groga uneix els valors de la funció de probabilitat binomial B_1000,1/2(n_c) que serveix per modelar aquest experiment. Vist l'histograma, si es compten 560 cares després de llançar una moneda 1000 vegades, la diferència amb el valor mitjà sí que és significativa. Es pot pensar amb raó que la moneda està trucada. La freqüència amb la qual surten 560 cares quan una moneda sense trucar es llança mil vegades es pràcticament zero. Es tan improbable que surtin 560 cares i només 440 creus que val més pensar que la moneda està trucada.

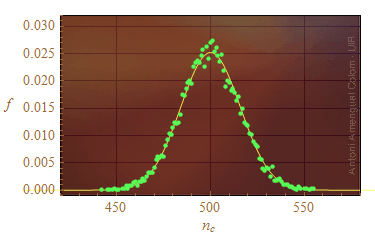
Figura 4. Els punts verds corresponen a la freqüència amb la qual han sortit n_c cares quan s'han fet mil llançaments simulats d'una moneda. Aquesta freqüència s'ha obtingut simulant 10000 repeticions dels mil llançaments. La línia groga és una distribució binomial que serveis de model teòric.

Figura 5. Els homes del Col·legi Estatal d'Agricultura de Connecticut s'han agrupat per altures formant columnes  (la imatge està extreta d'aquesta web on es dóna com a referència original: J. Heredity 5:511–518, 1914).

Els números de les sabates i les talles de la roba són conjunts numerables. Atès que no es pot mesurar tota la població, es fan mesures sobre una mostra i se suposa una funció de distribució adient que representi la població. Encertar amb les mides de sabates o jerseis que podrà vestir més gent té conseqüències econòmiques.

En moltes circumstàncies, la distribució normal o gaussiana serveix com a model teòric amb el que treballar matemàticament per donar resposta a qüestions pràctiques.

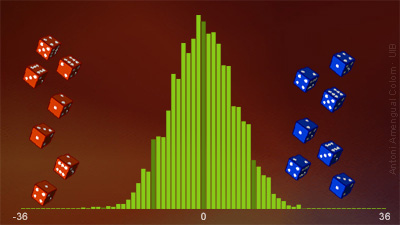
Figura 6. Histograma del resultat de prop de quatre mil llançaments per obtenir la suma dels punts de 7 daus blaus menys la suma dels punts de 7 vermells.

La distribució de probabilitat de la suma dels punts de n daus iguals amb cares equiprobables es pot calcular (veure tema), però el càlcul teòric no quedarà reproduït amb l'histograma dels resultats d'una determinada sèrie de llançaments (un histograma d'aquest tipus es pot generar amb la simulació del llançament de daus).

Una qüestió important és la de quantificar si la diferència entre l'histograma esperat i l'obtingut es deu a que el model teòric de la distribució no és apropiat. El text χ² s'usa per respondre aquesta qüestió.

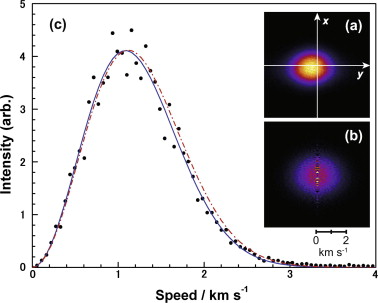
Figura 7. Dades experimentals ajustades per una funció de distribució de Maxwell-Boltzmann (ref.).

L'altura de les barres d'un histograma pot tenir error. A l'hora de comparar l'histograma obtingut amb l'esperat cal tenir present que el mètode amb que es determina la freqüència amb que es donen determinats valors pot ser incert. A la figura adjunta, s'usen punts en lloc de rectangles quan es pot pensar que la intensitat és proporcional a un nombre de molècules.

La mesura de les velocitats moleculars dóna un error sobre les velocitats i l'histograma pot ser irregular, l'histograma no és monòton allà on la distribució esperada sí ho és, per les fluctuacions aleatòries en el nombre de comptes i l'error experimental.