
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Distribució binomial
Definició de la funció de probabilitat binomial
Introducció «
El resultat d'un procés o un fenomen repetible que s'anomenarà experiment o mostreig és binomial si es compleixen aquestes tres condicions:
• Cada experiment és independent dels altres.
• Cada experiment només dóna un de dos resultats possibles, anomenats genèricament èxit i fracàs.
• La probabilitat d'èxit p és la mateixa en tots els experiments.
La funció de probabilitat binomial Bn,p(k) dóna la probabilitat de tenir k resultats d'èxit quan es fan n experiments.
Definició de la funció de probabilitat binomial «
L'expressió matemàtica de la funció de probabilitat binomial és
![]()
• El terme pk és la probabilitat que el resultat de k experimentes sigui èxit.
• El terme (1–p)n–k és la probabilitat que el resultat de n – k experiments sigui fracàs.
• El número binomial n sobre k dóna tots els casos en que això pot ocórrer i multiplica els altres dos termes perquè l'ordre en que surtin els resultats èxit o fracàs no importa.
A continuació es justifica la presència del coeficient binomial.
Combinacions de k èxits i n – k fracassos «
Es demostra a continuació que quan no interessa l'ordre en que es donen els resultats, k èxits i n – k fracassos es poden donar d'un nombre de maneres igual al valor del coeficient binomial n sobre k, el qual es defineix i s'escriu:
![]()
El símbol ! és el factorial del número que acompanya, n! és el producte del sencers des de n fins a 1.
Pas 1: Combinacions de lletres o bolles numerades
 «
«
S'analitzarà primer de quantes maneres es poden ordenar les lletres a, b, c i d.
Es pot posar qualsevol de les lletres al principi, qualsevol de les tres restants en segon lloc, una de les dues que no s'han posat en tercer lloc i la lletra que queda al final. Per tant, el nombre de possibilitats és 4×3×2×1. A la imatge següent es mostren les 24 ordenacions. Cada columna té la mateixa lletra inicial.

Figura 1. Les 24 possibles ordenacions de les lletres a, b, c i d.
Si es tingués una lletra més, hi hauria 5 opcions per a la lletra inicial. Llavors, per a les restants es tendrien les 24 opcions que ja s'han calculant per a quatre lletres. Hi haurà 5×24 ordenacions possibles de cinc lletres. Aquest recompte del nombre de casos es pot ampliar a un nombre de lletres w qualsevol per inducció. El nombre de maneres en que es poden ordenar w lletres és
w × (w – 1) × (w – 2) × ... × 3 × 2 × 1 = w!
Es poden considerar n bolles numerades en lloc de lletres. L'ús de lletres o números no canvia els resultats. Les n bolles es poden posar en fila de n! maneres diferents. Si n = 4, l'ordenació de les lletres de la Fig. 1 es pot usar directament per ordenar les boles identificant les lletres a, b, c i d amb els números 1, 2, 3 i 4, respectivament, i crear la Fig. 2.

Figura 2. Les 24 possibles ordenacions de 4 bolles numerades de l'1 al 4.
Pas 2: Combinacions de bolles de dos colors
 «
«
Si les bolles numerades són de dos colors, k blaves i n – k vermelles, de quantes maneres diferents per color es poden posar en fila una al costat de l'altra?
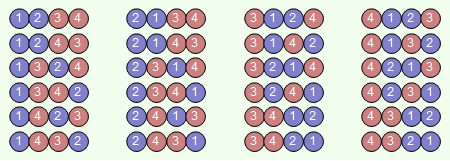
Figura 3. Les 24 possibles ordenacions de 4 bolles numerades de l'1 al 4 quan dues bolles són blaves i dues vermelles.
Les bolles es poden posar de n! maneres diferents segons els números (Fig. 3), però el nombre d'ordenacions és més petit quan només interessa el color. Un intercanvi de posició de dues bolles del mateix color no genera una ordenació diferent. En l'exemple de la Fig. 3, els intercanvis de les bolles 1 amb 2 i 3 amb 4 no donen seqüències de colors diferents. Dins el requadre de la Fig. 4, hi ha quatre ordenacions diferents segons els números de les bolles que són la mateixa quan només es mira el color.
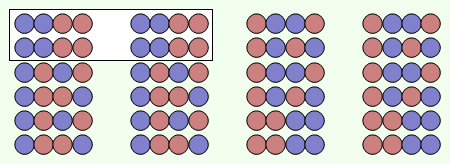
Figura 4. Les quatre ordenacions que hi ha dins el requadre són igual quan només es mira el color de les bolles.
Pas 3: Recompte
 «
«
Les k bolles de color blau es poden ordenar de k! maneres diferents i les n – k bolles de color vermell, de (n – k)! maneres diferents. Com que aquestes ordenacions donen la mateixa seqüència de colors, el nombre de seqüències diferents és
![]()
![]()
Per definició, el resultat d'aquest quocient és un número binomial i s'escriu de manera simbòlica
![]()
Les maneres d'ordenar n = 4 bolles, k = 2 vermelles i 2 blaves, són
![]()
Les sis ordenacions es mostren a la Fig. 5.
![]()
Figura 5. Les 6 ordenacions de dues bolles blaves i dues vermelles.
Quan es tenen n objectes iguals, només es poden ordenar d'una manera, per tant n sobre n ha de donar la unitat. L'expressió del número binomial donarà 1 si s'estableix que 0! = 1.
Triangle de Pascal «
Aplicant la definició a la suma de dos coeficients binomials seguits per a n > 1 es té
![]()
Si s'extreuen els factors comuns queda
![]()
Sumant les fraccions entre parèntesis i agrupant termes s'arriba al resultat
![]()
Però el darrer quocient es el número binomial n + 1 sobre k + 1, per tant
![]()
Aquesta relació serveix per construir el triangle de Pascal (també anomenat triangle de Tartaglia) mostrat a la Fig. 6. El valor de n augmenta per avall i el valor de k va des d'1 fins a n, d'esquerra a dreta. Els números es col·loquen de manera que el valor de (n + 1) sobre (k + 1) queda entre els resultats dels dos coeficients binomials de la fila anterior que sumats donen el mateix valor.
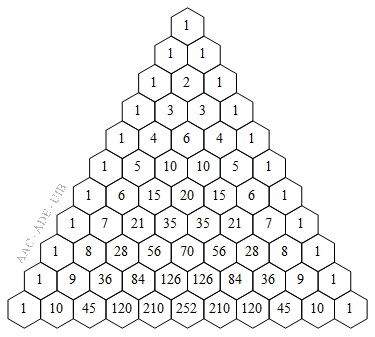
Figura 6. El triangle de Pascal fins a n = 11.
