Es considera una variable aleatòria X que pot prendre un valor numèric real x en un domini Ω = [a, b] per presentar les funcions densitat de probabilitat i distribució de probabilitat. Les dues funcions són bàsiques en els estudis de probabilitat i estadística. La primera funció es la derivada de la segona i la segona, la integral de la primera. La Fig. 1 il·lustra la segona relació.

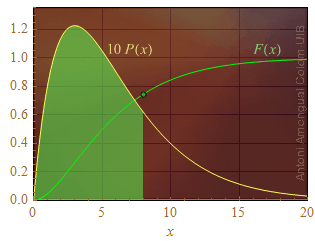
Figura 1. Representació de la densitat de probabilitat P(x) (línia groga) i la distribució de probabilitat F(x) (línia verda) d'una variable aleatòria positiva. L'àrea baix la corba P(x) des de l'origen fins a un punt x₀ és igual a F(x₀). La densitat de probabilitat s'ha multiplicat per 10 per fer-la més visible.

Es defineixen les notacions per a tres conceptes bàsics. La notació Pr(A) ja s'ha definit en el tema anterior per a variables aleatòries discretes, però s'inclou per mantenir el paral·lelisme de la presentació dels conceptes.

Pr(A) ≡ Probabilitat que succeeixi A

La notació Pr(A) s'usa per incloure la frase «probabilitat que succeeixi A» en una expressió o una fórmula. A serà del tipus «resultat més gran que 2», «resultat positiu», ...  Pr(A) no representa una funció.

Per a variables continues, no té sentit que A sigui «resultat igual a 2» perquè la probabilitat que la variable continua prengui un valor donat és zero. Després de les definicions es comenta aquest cas.

F(x) = Pr(X ≤ x)

La distribució de probabilitat per a una variable aleatòria continua X és la funció F(x) que dóna la probabilitat que X sigui menor o igual que x,

Com s'ha indicat en el tema anterior, la funció distribució es pot definir per a variables aleatòries discretes, però no se sol usar.

El nom de la variable aleatòria no es posa com subíndex de la lletra F si no hi ha d'haver confusió.

En anglès s'usen les sigles CDF per cumulative distribution function i es pot traduir per funció de distribució acumulada.

La densitat de probabilitat d'una variable aleatòria continua X és la funció

de manera que usant la lletra grega ξ per indicar la variable d'integració

En anglès s'usen les sigles PDF per probability density function i es pot traduir per funció densitat de probabilitat.

Les sigles D de CDF i PDF no signifiquen el mateix.

La probabilitat d'endevinar els punts que donarà un dau de sis cares abans de llançar-lo és superior al 16%. La d'endevinar la carta superior d'un manat de 48 cartes ben mesclat és aproximadament del dos per cent. Com més casos es puguin donar en un succés, menys probabilitats hi ha d'endevinar el resultat. La probabilitat que es doni un determinat resultat pot arribar a ser molt petita; però es pot calcular sempre que el nombre de casos sigui numerable.

En canvi, per a un succés amb la distribució de probabilitat d'una variable continua, no té sentit demanar amb quina probabilitat el resultat serà igual a un valor donat. La probabilitat és zero: és un cas límit de la regla de Laplace en que hi ha un cas favorable entre infinits casos possibles.

Mostra text vinyetes »

Amb les distribucions de probabilitat d'una variable aleatòria continua, s'ha de demanar per la probabilitat que el resultat sigui x₀ ± δ_x o que estigui entre uns valors x_min i x_màx. Només així s'obtendrà una probabilitat finita per comparar amb la d'altres resultats.

Si la funció P(x) és una funció densitat de probabilitat normalitzada coneguda, es pot calcular la probabilitat que x estigui dins l'interval [x_min, x_max] amb la integral

Si x_màx dista poc de x_min, la integral es pot aproximar directament per l'àrea del trapezi amb un costat igual al segment entre x_min i x_màx (apèndix). S'ha de multiplicar la longitud de la base per la semisuma de les altures, que és aproximadament el valor de la funció en el punt mitjà del segment dividit per dos

Les velocitats de les molècules d'un gas canvien per les col·lisions entre elles i amb les parets del recipient que conté el gas. Dins un recipient tancat a temperatura constant, hi ha un nombre de molècules aproximadament igual al valor que dóna l'equació del gas ideal,

on P és la pressió, V el volum, T la temperatura absoluta, N_A el nombre d'Avogadro i R la constant dels gasos. En un litre de gas a una atmosfera i 25 ºC, hi ha unes 2.5×10²² molècules. Són tantes que el nombre de les que tenen la velocitat dins un interval donat serà pràcticament al mateix en tot moment. Seran molècules diferents en temps distints, però això és irrellevant quan es considera el gas en conjunt.

Amb el gas en equilibri, hi ha molècules amb velocitats més grans que les d'altres molècules. Se sap que hi haurà col·lisions entre elles i les velocitats canviaran, però l'energia i el moment lineal totals es mantenen constants. James Clerk Maxwell i Ludwig Boltzmann estudiaren la distribució de les velocitats de les molècules d'un gas a temperatura absoluta T i calcularen la densitat

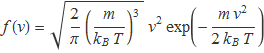
per al mòdul de la velocitat.^‡ En aquesta expressió, m és la massa de les molècules i k_B, la constant de Boltzmann (k_B = R / N_A). Es pot comprovar que les unitats de f(v) són (m/s)^–1.

La Fig. 1, mostra la funció f amb les abscisses escalades amb la velocitat que dóna el màxim de f(v), velocitat anomenada velocitat més probable, v_m.

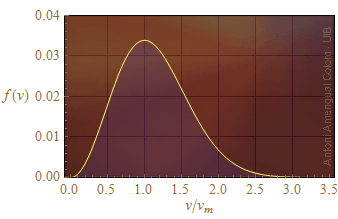
Figura 2. Densitat de probabilitat del mòdul de la velocitat de les molècules d'un gas.

La funció f(v) admet dues interpretacions. La integral de la distribució de Maxwell-Boltzmann entre dues velocitats v₁ i v₂, multiplicada pel nombre de molècules en el gas, dóna el nombre de molècules que tenen la velocitat entre v₁ i v₂ en qualsevol instant.

La funció f(v) també és pot considerar com una funció densitat de probabilitat per calcular la probabilitat que una molècula elegida a l'atzar tengui la velocitat entre v₁ i v₂,

Si bé no es durà a la pràctica l'elecció d'una molècula a l'atzar, es pot considerar i mesurar la velocitat de les molècules que escapen per un forat petit del recipient. Així és com es feren mesures experimentals per comprovar la validesa de la distribució de Maxwell-Boltzmann.

En tot cas, cal tenir present que no té sentit demanar per la probabilitat de trobar una molècula amb una velocitat v determinada, perquè és zero; com ja dóna la integral si els dos límits d'integració són iguals. Encara que hi hagi un nombre enorme de molècules en condicions normals, la quantitat és finita, mentre que les velocitats possibles són infinites.

Sempre s'ha de demanar la probabilitat que la velocitat estigui dins un interval, que pot ser el de la resolució de la mesura de les velocitats. Si v₁ = v₀ – δ_v/2 i v₂ = v₀ + δ_v/2, l'àrea sota la corba f(v) es pot aproximar per l'àrea del trapezi de base δ_v i altures f(v₀ – δ_v/2) i f(v₀ + δ_v/2),

Pr(v ∈ [v₀ – δ_v/2, v₀ + δ_v/2]) = f(v₀) δ_v.

Si la velocitat es mesura amb una resolució de dècimes d'unitat, δ_v = 0.05. De manera que quan es demani per la probabilitat que la velocitat sigui 12.7, s'ha d'entendre que es demana la probabilitat per a l'interval [12.65, 12.75]. Qualsevol valor dins aquest interval queda amb un decimal arrodonit a 12.7.

Exemple »