
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Teoria de la probabilitat
Introducció a les distribucions de probabilitat discretes
Introducció «
Es defineixen els conceptes bàsics de la probabilitat que una variable aleatòria X prengui un valor determinat d'un conjunt Ω = {x1, x2, ..., xn}.
Definicions «
Es defineixen les notacions per a tres conceptes bàsics.
Probabilitat que succeeixi A «
Pr(A) ≡ Probabilitat que succeeixi A
La notació Pr(A) s'usa per incloure la frase «probabilitat que succeeixi A» en una expressió o una fórmula. A serà del tipus «resultat igual a 2», «resultat més gran que 2»... Pr(A) no representa una funció.
Funció de probabilitat «
![]()
La funció de probabilitat per a una variable aleatòria discreta és la funció PX(x) que dóna la probabilitat que X sigui igual a x. El nom de la variable aleatòria no fa falta en el subíndex de la lletra P si no hi ha d'haver confusió.
Distribució de probabilitat
 «
«
FX(x) = Pr(X ≤ x) (si els valors del conjunt X estan ordenats).
Per a una variable aleatòria discreta que pot prendre valors dins un conjunt ordenat, es pot definir la distribució de probabilitat FX(x) per tenir la probabilitat que X sigui menor o igual que x,
![]()
Els valors del conjunt poden sorgir d'un espai amb una regla d'ordenació «més petit que» ja definida. Això passarà quan els valors siguin números o lletres. Si la regla no existeix, per exemple per als elements del conjunt d'accions {saltar, cantar, llegir, riure} que hagi de fer una persona, es pot establir la regla a partir de l'ordre com s'escrigui el conjunt.
El nom de la variable aleatòria no fa falta en el subíndex de la lletra F si no hi ha d'haver confusió.
Exemple
 «
«
La suma S dels punts que es poden obtenir al llançar dos daus de sis cares està entre 2 i 12. La suma és una variable aleatòria discreta perquè els valors possibles es poden enumerar.
Les cares només poden quedar de 36 maneres diferents, totes igualment probables si els daus no estan trucats. És immediat comptar en quants de casos surt cada un dels resultats: per ordre de 2 a 7 punts surten 1, 2, 3, 4, 5 i 6 casos; i de 8 a 12 punts surten 5, 4, 3, 2 i 1 casos. Amb la regla de Laplace, la probabilitat d'obtenir una suma S serà
![]()
Aquesta funció P(S) és la distribució de probabilitat per a la suma de dos daus llançats a l'atzar. La funció només té valors definits per a S ∈ [2, 12].
| S | P(S) | F(S) |
| 2 | 1/36 | 1/36 |
| 3 | 2/36 | 3/36 |
| 4 | 3/36 | 6/36 |
| 5 | 4/36 | 10/36 |
| 6 | 5/36 | 15/36 |
| 7 | 6/36 | 21/36 |
| 8 | 5/36 | 26/36 |
| 9 | 4/36 | 30/36 |
| 10 | 3/36 | 33/36 |
| 11 | 2/36 | 35/36 |
| 12 | 1/36 | 36/36 |
Taula 1. Funció de probabilitat i distribució de probabilitat de la suma dels punts de dos daus.
En lloc de la suma dels punts, es podria usar la mitjana s = S/2 com a la variable aleatòria d'interès. La distribució de probabilitat P(s) estaria definida per als valors s ∈ [1, 6]. Una representació d'aquesta funció es mostra a la Fig. 1.
L'anàlisi de les sumes amb més daus s'analitza en el tema Funció de probabilitat de la suma dels punts de n daus.
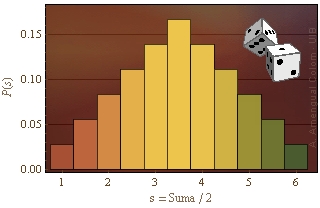
Figura 1. Distribució de probabilitat de la mitjana dels punts de dos daus.
