En aquest tema es demostra que la funció densitat de probabilitat d'una variable u calculada amb una funció u(x) a partir dels valors x₁ d'una variable aleatòria gaussiana X₁ de mitjana μ₁ i desviació estàndard σ₁ quan u(x) es pot aproximar per una funció lineal prop de μ₁, és una funció gaussiana de variància

Sigui X₁ una variable aleatòria gaussiana amb la funció densitat de probabilitat

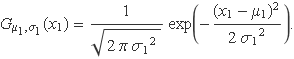
Es vol trobar la funció densitat de probabilitat de

La solució no és senzilla en el cas general, però quan u(x₁) es pot aproximar per una funció lineal allà on la funció densitat de probabilitat de x₁ té valors significatius, la solució és gaussiana. La demostració d'aquest fet es dóna a continuació.

La funció u(x) aproximada per la sèrie de Taylor a primer ordre al voltant de μ₁ és

La funció queda així aproximada per la relació lineal

on c₁ és la constant

Usant la relació lineal entre u i x, la variable aleatòria u tendrà la mateixa variància σ que la variable aleatòria c₁ x₁ perquè la constant c₀ no té cap efecte sobre la variància. Per tant, la variància de la variable u és igual a la variància d'una variable aleatòria gaussiana multiplicada per una constant

És important tenir present que aquest resultat és aproximat i que l'aproximació és bona en la mesura que la sèrie de Taylor a primer ordre de la funció u és una bona aproximació dins l'interval x₁ ± σ₁.

Per il·lustrar la condició imposada i el resultat de la secció anterior per a una variable aleatòria continua, es presenta primer una il·lustració amb una variable aleatòria discreta. La comprensió de la Fig. 1 permetrà entendre bé la il·lustració de la secció següent.

Sigui X una variable aleatòria discreta que pren valors sencers de l'espai mostral {5, 6, 7, ..., 15}. La funció de probabilitat F_X(ν) es representa amb l'histograma de color verd a la Fig. 1.

Quina és la funció de probabilitat F_U(u) de la variable aleatòria U calculada aplicant una funció u(ν) als valors de la variable aleatòria X?

L'espai mostral de la variable U serà {u(5), u(6), u(7), ..., u(15)} i es té

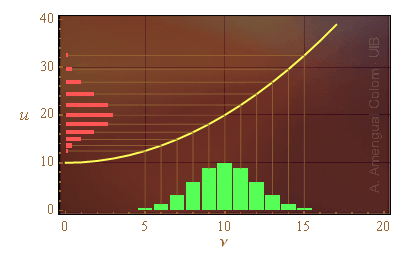
Figura 1. Els histogrames representen les funcions de probabilitat d'una variable aleatòria X (verd) i una variable aleatòria U = u(X) (vermell). La línia groga representa la funció u.

Si la variable aleatòria X és continua, s'ha de cercar una relació entre les funcions densitat de probabilitat. En tal cas, es complirà que

La línia groga a les Figs. 2a i b representa certa funció u(x).   

La línia verda representa una funció de distribució de probabilitat gaussiana. La variància σ₁ d'aquesta funció a la Fig. 2a és més gran que a la Fig. 2b. La mitjana μ₁ no canvia.

La línia vermella representa la funció de distribució de probabilitat dels valors u(x).

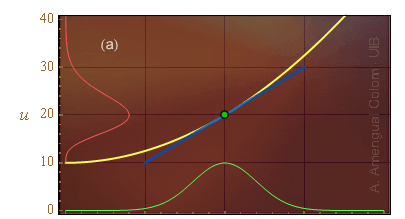
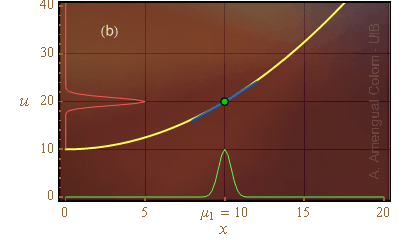
Figura 2. Veure descripció en el text.
a) La corba vermella no és simètrica, per tant no pot ser una funció gaussiana.
b) La corba vermella se sembla bastant a una gaussiana.

La funció densitat de probabilitat de la Fig. 2a no compleix la condició establerta a la demostració de la secció anterior. La funció u(x) no es pot aproximar per una funció lineal (línia blava) allà on la funció densitat de probabilitat de x₁ té valors significatius. L'expressió de la funció de distribució de probabilitat d'u(x) no és senzilla. Es veu que la línia vermella no és simètrica respecte a una línia horitzontal que passés pel màxim.

La funció densitat de probabilitat de la Fig. 2b sí compleix la condició establerta a la demostració de la secció anterior. La funció u(x) es pot aproximar per una funció lineal (línia blava) allà on la funció densitat de probabilitat de x₁ té valors significatius. En conseqüència la funció de distribució de probabilitat de la variable u es pot aproximar bé per una funció gaussiana, la mitjana i la variància de la qual són

μ = u(μ₁),

σ = u'(μ₁) σ₁.