
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Distribució normal (gaussiana)
Norma, mitjana, variància i desviació estàndard
Introducció «
La funció de la variable x
![]()
amb a i b dos números reals, s'anomena funció gaussiana. Multiplicada per una constant perquè la integral sobre el domini valgui la unitat és la funció de densitat de probabilitat gaussiana, o com es diu àmpliament, la funció densitat de probabilitat normal. A continuació, es calcularan tres paràmetres fonamentals.
• La norma
![]()
• El valor esperat de x, el qual s'identifica amb la lletra μ.
![]()
• La variància de x, la qual s'identifica amb σ2; i la desviació estàndard, σ.
![]()
Es trobarà que
![]()
A la vista d'aquests resultats, la funció gaussiana normalitzada de mitjana μ i desviació estàndard σ dóna la funció densitat de probabilitat gaussiana
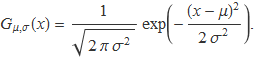
Norma  «
«
La constant de normalització CN de la funció
![]()
és igual a la integral de la funció g sobre tot el domini,
![]()
Per resoldre la integral es fa el canvi de variable
![]()
El canvi s'ha de fer en els dos límits d'integració, la funció i la diferencial,
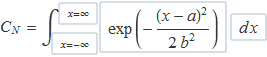
Els límits segueixen essent ±∞, el canvi de variable de la funció és trivial i dx = b dz,
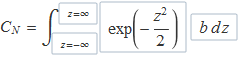
Aquesta integral es pot resoldre amb tècniques de càlcul avançat o relacionant el seu quadrat amb una integral doble (veure apèndix amb aquest càlcul). El resultat és
![]()
La constant de normalització és
![]()
S'ha de notar que com que l'arrel de 2π és aproximadament 2.5, el màxim de g(x)/CN és aproximadament 0.4.
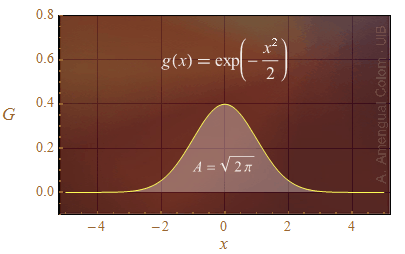
Figura 1. La línia groga representa la funció gaussiana centrada a l'origen d'abscisses. El valor del màxim de la funció és proper a 0.4.
Mitjana  «
«
El valor esperat de x és
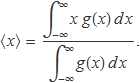
Atès que la funció g(x) és simètrica respecte a x = a, la mitjana serà a. Això és el que es demostrarà a continuació fent el càlcul de la integral.
La integral del denominador dóna CN com s'ha vist a l'apartat anterior. Per tant,
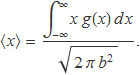
La integral del numerador es resol amb el canvi de variable
![]()
Es tendrà
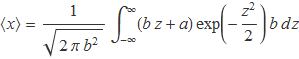
La integral se separa en dues:
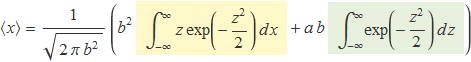
La integral del primer terme requadrat en color és
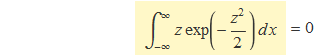
perquè la funció és imparell i l'interval d'integració és parell (Fig. 2). La integral del segon terme requadrat en color ja ha sortit a l'apartat anterior i val

Simplificant de manera directa queda
![]()
El paràmetre a de la funció gaussiana és igual a la mitjana de les x i s'identifica usualment amb la lletra grega μ.

Figura 2. El producte d'una funció parell (la gaussiana) per una funció imparell (x) dóna una funció imparell. La integral de la funció imparell sobre tot l'eix x és 0 perquè l'àrea entre la funció i l'eix x negatiu (zona groga) és igual i de signe contrari a l'àrea entre la funció i l'eix x positiu (zona blava).
Variància i desviació estàndard  «
«
La desviació estàndard al quadrat o variància de la funció
![]()
és el resultat de
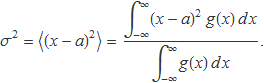
La integral del denominador dóna la constant de normalització CN que ja s'ha calculat en el primer apartat. Així es té
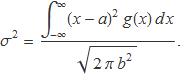
La integral del numerador es resol amb el canvi de variable
![]()
Es tendrà dx = b dz i
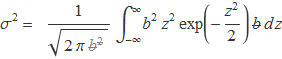
Es farà una integració per parts
![]()
amb la identificació

La derivada i la primitiva d'aquestes funcions són trivials:
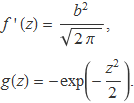
Realitzant la integració per parts es tendrà:
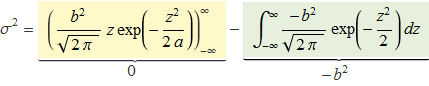
El primer terme és zero perquè l'exponencial va a zero més ràpid que z a infinit i el límit de la funció z2 exp(–z2/2a) és zero per a z → ±∞. El segon terme sense els factors constants és la integral que dóna arrel de 2π. Així la variància és igual al paràmetre b2 i la desviació estàndard és b:
![]()
La desviació estàndard ubica la posició dels punts d'inflexió de la corba de la funció densitat de probabilitat normal.
Figura 3. Il·lustració de l'efecte del canvi de la mitjana i de la desviació estàndard sobre la funció densitat de probabilitat gaussiana o normal.
