Es dóna una demostració que la integral gaussiana (la integral impròpia amb els límits d'integració de menys a més infinit de la funció gaussiana) val

La demostració es farà en dues passes. En lloc de calcular la integral gaussiana es calcularà el seu quadrat. La demostració presentada es basa en que una integral doble del producte de dues funcions, una de cada una de les variables d'integració, és igual al producte de les integrals de cada funció,

Aquesta propietat s'aplicarà dos pics en la demostració.

Sigui I el valor de la integral de la gaussiana:

El resultat d'una integral és el mateix sigui quin sigui el nom de la variable d'integració. Per tant, es pot escriure

El quadrat de I és pot expressar multiplicant la integral de la gaussiana per ella mateixa, però amb una integral escrita usant la variable x i l'altra, usant la variable y:

Per la propietat (1) de les integrals dobles, es pot escriure

o, sumant els exponent,

El domini d'aquesta integració es pot visualitzar com tot el pla x-y. Aquest és un punt crucial perquè dóna la idea de recórrer el domini usant coordenades polars r i φ. El radi anirà de 0 a ∞ i l'angle, de 0 a 2π.

Per fer un canvi de variables en una integral doble s'ha d'usar l'anomenat jacobià de la transformació. En el cas de coordenades cartesianes a polars el canvi és

Mostra justificació »

En coordenades polars

x² + y² = r²

i la integral I² sobre tot el pla és

S'usa per segona vegada (1), ara per separar la integral en dos termes,

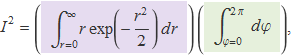
els quals es determinen amb facilitat:

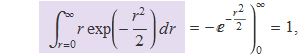
D'aquesta manera resulta

I² = 2 π

i només queda fer l'arrel quadrada per tenir el valor de I, la integral gaussiana.