
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Apèndix
Integració per parts
Introducció «
La integració per parts és un mètode aplicat quan la integral es pot posar en la forma
![]()
on la funció g(x) es fàcil de determinar a partir de la derivada.
El mètode s'aplica usant la fórmula
![]()
i és útil quan la integral de la dreta és pot realitzar més fàcilment que la original.
Demostració de la fórmula de la integració per parts «
La derivada del producte de dues funcions és
![]()
Aïllant el darrer terme es troba
![]()
La integració d'aquestes funcions en un interval (a, b) dóna
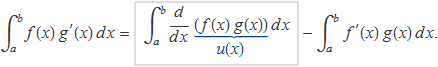
La primera integral definida de la dreta, inclosa dins un requadre, és
![]()
Així, s'arriba al resultat
![]()
Exemple: Integral de la forma xn exp(-a x) amb a > 0
 «
«
La integració per parts en alguns casos s'ha de realitzar repetidament fins que la integral que queda a la dreta es pot resoldre directament. Aquest és el cas de la integral que es considera com exemple quan n > 1.
Integral de x exp(-a x)
 «
«
Es calcularà la integral
![]()
usant la fórmula de la integració per parts.
S'identifica
![]()
Trobar g és fàcil perquè
![]()
Al fer la integració per parts
![]()
es troba
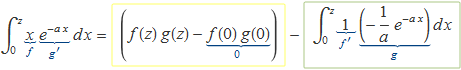
Escriure el resultat dels dos termes emmarcats és immediat. El primer terme dóna
![]()
El segon terme és la integral d'una exponencial i dóna
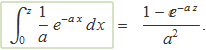
Sumant els dos termes s'obté finalment
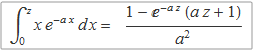
La integral impròpia amb z→ ∞ val
![]()
Integral de x2 exp(-a x)
 «
«
Es calcularà la integral següent usant la fórmula de la integració per parts:
![]()
S'identifica
![]()
La funció g s'ha determinat a l'exemple anterior quan, precisament, s'ha integrat g':
![]()
Al fer la integració per parts
![]()
es troba
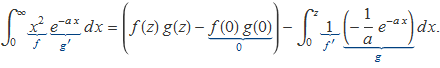
La integral que queda per fer és la d'una exponencial senzilla. S'obté al final
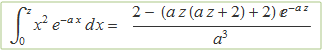
La integral impròpia amb z→ ∞ val
![]()
Integral impròpia de xn exp(-a x)
 «
«
Les integrals impròpies dels dos exemples anteriors, són casos particulars de
![]()
Les integrals definides de les funcions xn exp(–a x), amb n sencer, es resolen repetint la integració per parts.
