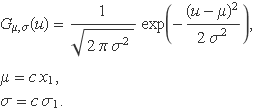Es demostrarà en aquest tema que la funció densitat de probabilitat d'una variable aleatòria gaussiana de mitjana μ₁ i desviació estàndard σ₁, multiplicada per una constant c, també és gaussiana amb mitjana c μ₁ i desviació estàndard c σ₁.

Siguin X₁ una variable aleatòria gaussiana. La funció densitat de probabilitat és

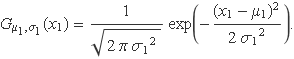
Donada una constant c, es vol trobar la funció densitat de probabilitat de la variable

u = c x₁.

La probabilitat d'obtenir un valor

és igual a la probabilitat que x₁ tengui un valor

Si δ_u és petit, aquesta probabilitat es pot aproximar pel valor de la funció gaussiana en el centre de l'interval multiplicat per l'amplada de l'interval,

Aquesta aproximació ja s'ha usat abans. Estrictament s'hauria d'integrar la distribució gaussiana; però quan l'interval d'integració és petit, la integral es pot aproximar per l'àrea d'un trapezi, la base del qual està sobre l'eix d'abscisses. La longitud d'aquesta base s'ha de multiplicar per la semisuma de les altures, que és aproximadament igual al valor de la gaussiana en el centre de l'interval.

La part exponencial de la funció gaussiana es pot escriure en la forma

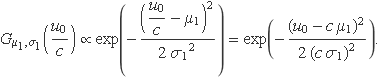
Per tant, la probabilitat d'obtenir un valor u = u₀ ± δ_u és

El factor de proporcionalitat δ_u es pot deixar de banda perquè no contribueix a la funció densitat de probabilitat normalitzada. La funció que multiplica a δ_u en l'expressió anterior és la funció densitat de probabilitat directament en termes de la nova variable u,