
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Distribució normal (gaussiana)
Estimació de la mitjana i la variància a partir d'un conjunt de dades
Introducció «
Es pretèn donar una estimació de la mitjana i de la variància d'una població amb distribució gaussiana a partir d'una mostra de n valors a1, a2, a3, ..., an.
L'estimació es farà cercant els paràmetres μ i σ de la distribució gaussiana que maximitzen la probabilitat Pmostra d'haver obtingut els valors de la mostra.
El valor de la mitjana es trobarà fàcilment i serà
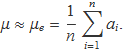
El valor de la variància no es podrà obtenir tan fàcilment. L'intent de fer una estimació de la variància amb el valor que maximitza Pmostra té el problema que la resposta queda en funció de la mitjana de la població, la qual és desconeguda. Només és té l'estimació feta a partir de la mostra. En conseqüència, és necessari fer un altre anàlisi per obtenir la variància. Es demostrarà que l'estimador estadístic de la variància d'una població amb distribució gaussiana és
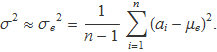
Si es conegués la mitjana de la població i no s'hagués d'usar μe,

seria un estimador estadístic sense biaix adient.
La probabilitat d'obtenir una mostra determinada
 «
«
Les calculadores generen un número pseudoaleatori entre 0 i 1 cada pic que s'executa la funció RAN#. El número obtingut no és realment aleatori perquè la calculadora empra un algoritme per calcular-lo i es pot generar la mateixa seqüència partint d'un número inicial fixat. Per això es parla de números pseudoaleatoris.
El conjunt de valors aleatoris creats amb la tecla RAN# estan distribuïts homogèniament en l'interval (0, 1). És fàcil imaginar que hi podria haver una tecla per generar valors aleatoris segons una distribució gaussiana. Suposem que aquesta tecla existís i que algú ha definit la mitjana i la variància de la distribució sense anunciar els valors. Quina estimació es podria fer de la mitjana i de la variància a partir de n valors generats?
Suposem que s'han anotat n valors, cada un dels quals s'identifica amb la lletra a i un subíndex,
{a1, a2, a3, ..., an}.
La probabilitat Pi d'obtenir un valor x dins un interval ai ± δx de manera que el número arrodonit s'escrigui com ai és
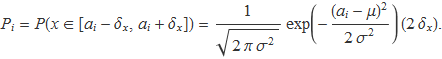
Estrictament s'hauria d'integrar la distribució gaussiana entre ai – δx i ai + δx; però quan l'interval és petit, la integral es pot aproximar per l'àrea d'un trapezi, la base del qual està sobre l'eix d'abscisses i té longitud 2 δx (apèndix). Aquesta longitud s'ha de multiplicar per la semisuma de les altures, (Gμ,σ(ai – δx) + Gμ,σ(ai + δx))/2 que és aproximadament igual a Gμ,σ(ai) per a δx petit.
Cal notar que no se cerca la probabilitat que el dispositiu doni un determinat valor en pitjar el botó, se cerca la probabilitat que el dispositiu doni concretament els n valors obtinguts. La probabilitat d'obtenir el conjunt particular de valors a1, a2, a3, a4, ..., an és el producte
Pmostra = P1 × P2 × P3 × ... × Pn.
El fet que les probabilitats Pi no es poden calcular numèricament perquè no es coneix la mitjana ni la variància, no impedeix tenir una expressió útil amb la que treballar i resoldre el problema. Prescindint dels factors numèrics comuns, es té
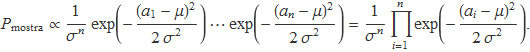
El producte d'exponencials dóna l'exponencial de la suma dels exponents
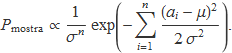
La variància és desconeguda, però en aquest cas és una constant i surt fora del sumatori per donar
Pmostra ∝ F(μ, σ)
on
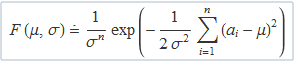
L'estimació de la mitjana i de la variància es farà cercant els valors que fan màxima la probabilitat Pmostra. Per tant, els valors han de sortir de la resolució de
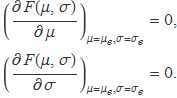
La primera equació igualada a zero es pot resoldre independentment de l'altra. Per tant, es resoldrà primer ella tota sola. Però abans de procedir a la resolució de les equacions, es presenten les figures 1 i 2 que il·lustren la probabilitat i la seva variació al canviar la mitjana i la variància. Si es tingués un altre conjunt de punts, la mitjana i la variància serien segurament diferents, però s'ha de fer alguna suposició per aconseguir l'estimació més probable.
Figura 1. La probabilitat Pmostra d'un conjunt de punts és màxima quan es calcula amb la distribució gaussiana que té el paràmetre μ igual al la mitjana dels punts. La fletxa verda marca la posició de la mitjana dels 7 punts verds. Pmostra és proporcional a l'àrea de les 7 columnes taronja.
Figura 2. La probabilitat Pmostra d'un conjunt de punts és màxima quan es calcula amb la distribució gaussiana que té el paràmetre μ igual al la mitjana dels punts i la variància σe. La fletxa verda marca la posició de la mitjana dels 7 punts verds i les línies verticals verdes les de μe ± σe. Els punts blancs són els punts d'inflexió de la gaussiana dibuixada. Pmostra és proporcional a l'àrea de les 7 columnes taronja.
Estimació de la mitjana μ de la distribució gaussiana
 «
«
L'estimació μe de la mitjana μ a partir del conjunt de valors {a1, a2, a3, ..., an} serà el valor que faci màxima la probabilitat d'haver obtingut el conjunt de valors, llavors s'ha de complir
![]()
Començant a fer la derivada de l'exponencial es troba
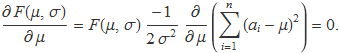
L'equació mostra que l'extrem de l'exponencial es correspon amb un extrem de l'exponent. El valor de la variància és irrellevant. Com que l'exponent és negatiu, l'exponencial tendrà el valor màxim quan el sumatori sigui mínim. Fent la derivada del sumatori de l'exponent es tendrà
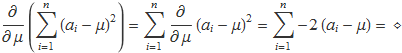
Usant les propietats del sumatori
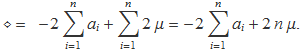
La derivada avaluada a μ = μe i igualada a zero dóna l'equació
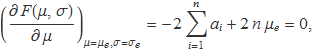
de la qual es pot aïllar μe, que tendrà el valor de la mitjana del conjunt de n valors ai,
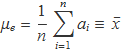
La millor estimació que es pot calcular de la mitjana de la distribució gaussiana a partir de n valors aplicant el principi de màxima probabilitat és la mitjana de la mostra.
Figura 3. La línia groga representa la distribució gaussiana d'un conjunt molt gran de valors. Les abscisses dels n punts verds representen valors extrets aleatòriament (les ordenades són arbitràries per separar els punts quan n es gran). La fletxa verda marca la mitjana dels n punts. A mesura que n creix, la mitjana d'una mostra se sembla amb més freqüència a la mitjana de la població, 0 en aquest exemple.
Estimació de la variància σ de la distribució gaussiana (estimador esbiaixat)
 «
«
L'estimació σe de σ a partir del conjunt de valors {a1, a2, a3, ..., an} serà el valor que faci màxima la probabilitat d'haver obtingut aquest conjunt de valors. El valor de σe es determinarà amb l'equació
![]()
Per simplificar la notació, convé definir
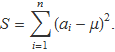
La derivada serà
![]()
L'únic terme que es pot anul·lar és el primer
![]()
Canviant S pel sumatori que representa, s'obté
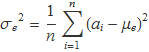
Encara que no es demostri aquí, σe2 és un estimador estadístic amb biaix de la variància. Un estimador sense biaix s'aconsegueix canviant n per n – 1 en el denominador. En el pròxim apartat es demostra com s'obté aquest estimador sense biaix.
Estimació de la variància σ de la distribució gaussiana amb la variància de la mostra
 «
«
Considerem el conjunt de valors {a1, a2, a3, ..., an} i la suma‡
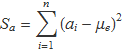
on
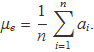
Expandint (ai – μe)2, es tendrà
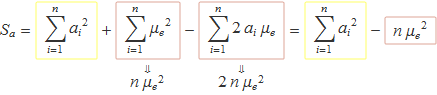
Els sumatoris que es multiplicaran per desenvolupar el quadrat d'un sumatori com μe s'han d'escriure amb índex muts diferents,
 .
.
Realitzant els productes queda
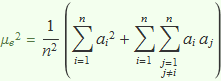 .
.
La suma Sa es pot escriure usant l'expressió de μe presentada en el requadre sobre aquestes línies. En el sumatori sobre j només es posarà j ≠ i per simplificar la notació,
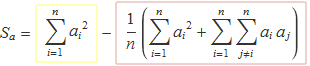
Agrupant els dos sumatoris amb ai2 es té

Per a una altra seqüència de n valors {b1, b2, b3, ..., bn} es trobaria de manera similar
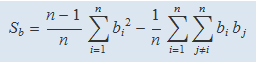
I per a una altra seqüència {c1, c2, c3, ..., cn},
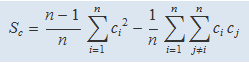
El valor mitjà dels tres sumatoris és
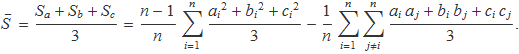
Per escriure l'expressió del valor mitjà amb un nombre L de seqüències qualsevol, se suposarà que la darrera seqüència s'identifica amb la lletra z i les que queden enmig, d'alguna manera que no fa falta especificar. La mitjana de les L seqüències és
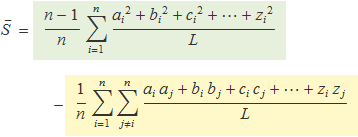
Avaluació del primer sumatori
 «
«
Aquí es mostrarà que el primer sumatori, que s'anomenarà Σ1 val
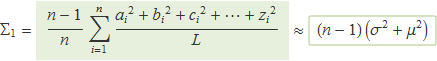
El sumatori té n × L sumands:
![]()
Aquesta suma dividida per L s'acosta a la mitjana del quadrat de la variable per a L gran, mitjana que es pot relacionar amb la variància i la mitjana de la distribució gaussiana amb operacions semblants a les que s'han fet per desenvolupar Sa al principi d'aquest tema. Per definició,
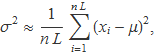
i desenvolupant el quadrat i el sumatori com ja s'ha mostrat abans, s'obtendrà
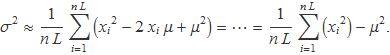
Aïllant el sumatori de xi2 queda
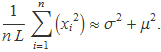
Usant aquesta relació, s'obté
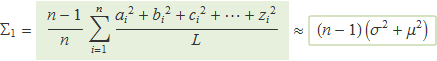
Avaluació del segon sumatori
 «
«
Aquí es mostrarà que el segon sumatori, que s'anomenarà Σ2 val
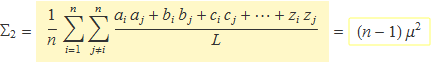
Es defineixen unes noves variables εa,i tals que ai = μ + εa,i, de manera que
![]()
Substituint aquesta expressió dins el sumatori apareixeran tres tipus de termes:
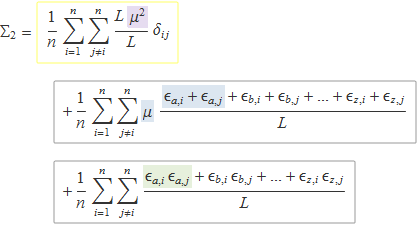
Els dobles sumatoris dels requadres grisos es poden negligir per a L gran perquè els valors de εa,i = ai – μ seran positius i negatius, i hi haurà una quantitat de valors semblants a una banda i l'altra de la mitjana de manera que els termes dels numeradors es cancel·laran pràcticament uns amb els altres.
Només el primer doble sumatori, en el requadre groc, contribueix a Σ2. L'índex i pren n valors i l´índex j, n – 1 perquè s'han d'excloure els termes j = i. Queda així
![]()
El resultat
 «
«
Finalment, substituint l'avaluació dels dos sumatoris feta, la mitjana de S queda
![]()
Fet un mostreig de n valors, es pot calcular la suma
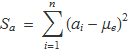
Si el mostreig es repeteix un nombre L molt gran de vegades, la mitjana de les sumes Sx és
![]()
Llavors,
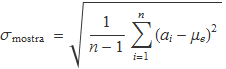
Exemple
 «
«
A la figura següent s'il·lustra el que s'ha descrit en el darrer apartat. S'han generat L = 10 sèries de n = 100 valors. Els valors s'han usat com abscisses d'uns punts. S'han donat ordenades arbitràries als punts per separar-los verticalment i fer-los visibles. Les puntes grogues mostren els valors mitjans de les sèries. La línia vermella és el valor mitjà de la distribució gaussiana. El número a la dreta de cada quadre és
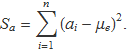

Figura 4. L = 10 sèries de n = 100 valors aleatoris. Els valors s'han generat a partir d'una distribució gaussiana de variància 1 (la separació entre les línies verticals blanques és també 1). Les puntes grogues marquen la mitjana de cada mostra (la mitjana de la funció gaussiana està sobre la línia vermella). Els números de la dreta s'expliquen en el text.
La desviació estàndard de la distribució gaussiana es podria avaluar a partir de la mitjana de les Sa si es tinguessin moltes sèries de n valors. Amb 10 sèries es pot pensar que es té una aproximació. Amb els 10 valors de la figura es té
![]()
L'estimació de la variància serà
![]()
valor proper a 1. En cas de tenir només una mostra, s'hauria de donar l'estimació usant la suma Sa.
