
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Propagació dels errors aleatoris
Variables calculades amb funcions de dues o més variables aleatòries gaussianes
Introducció «
En aquest tema es demostra que la funció densitat de probabilitat d'una variable u que es calcula amb una funció u(x1, x2, ...., xn) a partir dels valors xi de n variables aleatòries gaussianes Xi de mitjana μi i desviació estàndard σi quan la funció u es pot aproximar per un desenvolupament en sèrie de Taylor a primer ordre prop dels valors xi = μi, és una funció gaussiana de variància
![]()
on el subíndex μ indica que les derivades s'han d'avaluar amb els valors xi = μi amb i = 1..n. Usant el símbol sumatori, l'expressió per a la desviació estàndard de la gaussiana és
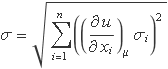
Demostració
 «
«
Siguin {X1, ..., Xn} un conjunt de n variables aleatòries gaussianes amb les funcions densitat de probabilitat
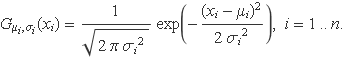
Es vol trobar la funció densitat de probabilitat de la variable
![]()
La funció densitat de probabilitat no té una expressió senzilla en el cas general, però és gaussiana quan la funció u es pot aproximar pel desenvolupament en sèrie de Taylor allà on les funcions densitat de probabilitat de totes les xi tenen valors significatius. La demostració d'aquest fet es dóna a continuació.
La funció u aproximada per la sèrie de Taylor a primer ordre al voltant dels valors xi = μi és
![]()
El subíndex μ indica que les derivades s'han d'avaluar amb xi = μi, i = 1..n. Cada derivada parcial dóna un valor constant
![]()
Amb aquestes constants, en lloc de l'expressió exacta de la funció u, els valors es poden calcular usant l'aproximació
u(x1, x2, ..., xn) ≈ c0 + c1 x1 + ... + cn xn.
Aquesta és una suma de variables aleatòries gaussianes multiplicades per constants. El valor de la variable u es calcula amb una combinació lineal de variables aleatòries gaussianes. La funció densitat de probabilitat de la variable u és gaussiana amb
![]()
És important tenir present que aquest resultat és aproximat i que l'aproximació és bona en la mesura que la sèrie de Taylor a primer ordre de la funció u és una bona aproximació per els valors xi que donen valors significatius de Gμi,σi(x), i = 1..n.
