
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Covariància i correlació lineal
El coeficient de correlació lineal
Introducció «
Per a un conjunt de parelles de valors {xi, yi}, i = 1..n, obtingudes en una sèrie de mesures, es defineix el coeficient de correlació lineal
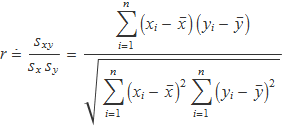
Dos usos del coeficient de correlació lineal
 «
«
A vegades sabem que hi ha una relació lineal entre dues variables i a vegades volem descobrir si existeix la relació lineal entre elles. El coeficient de correlació lineal serveix per quantificar la linealitat de la relació entre dues variables. Si se sap que la relació lineal existeix, el coeficient serà un indicatiu de la qualitat de la mesura. Si es desconeix l'existència d'una relació lineal, les mesures poden servir per descobrir que hi ha una relació lineal entre les variables i, en algun cas, cercar el motiu de perquè existeix tal relació.
Que existeixi una correlació lineal entre els valors de dues magnituds x i y no implica que hi hagi una relació causal entre les magnituds. Per exemple, si x i y són les densitats de dos fluids dins recipients sobre la mateixa estufa i es mesuren les densitats per a diferents temperatures d'un interval acotat, es trobarà que les densitats estan correlacionades linealment. No existeix cap relació entre les densitats de dos fluids diferents. La causa de la correlació és senzillament que les dues densitats depenen de la temperatura.
A vegades sabem que hi ha una relació lineal entre dues variables...
 «
«
El període de les oscil·lacions de petita amplitud d'una objecte feixuc penjat del sòtil per un fil de longitud x serà igual al d'un pèndol simple,
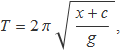
on g és l'acceleració de la gravetat i c la distància de l'extrem inferior del fil al centre de masses de l'objecte. Elevant l'expressió al quadrat s'obté una expressió del tipus
T2 = a x + b
amb
![]()
Quan es mesuri el període amb fils de diferent longitud, hi haurà una relació lineal entre el quadrat del període i la longitud del fil i un ajust per mínims quadrats proporcionarà els coeficient de la recta. El pendent es podrà usar per fer una determinació de l'acceleració de la gravetat. Si el coeficient de correlació lineal no és bo, significarà que la mesura feta és pobra.
... i a vegades volem descobrir si existeix la relació lineal entre dues variables.
 «
«
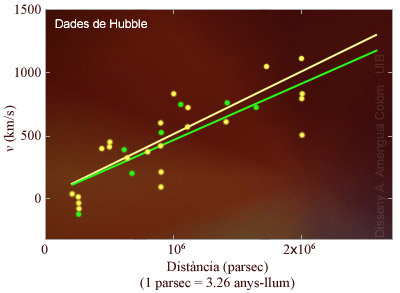
Figura 1. Gràfic dissenyat sobre l'original que publicà Edwin Hubble: «Relació velocitat-distància per a galàxies i clústers de galàxies distants. Els punts grocs representen galàxies, i la línia groga representa la recta que millor els ajusta. Els punts verds representen clústers de galàxies, i la línia verda és la recta que els ajusta millor.»
Els electrons dels àtoms estan en orbitals d'energia definida i quan un electró passa d'un nivell d'energia alta a un d'energia més baixa, emet radiació electromagnètica de freqüència proporcional a la diferència. Una làmpada amb hidrogen a l'interior emet llum visible de 410 nm, 434 nm, 486 nm i 656 nm. També emet altre radicació però amb longituds d'ona que l'ull humà no percep.
De manera simètrica, un electró només pot absorbir radiació electromagnètica de les mateixes freqüències que pot emetre. Amb l'absorció d'energia, l'electró passa d'un nivell a un altre. El model atòmic de Bohr permeté descriure les freqüències dels espectres d'emissió i d'absorció dels àtoms.
Quan la llum d'una estrella recollida amb un telescopi se separa usant un prisma o un altre dispositiu espectroscòpic i no es troba llum vermella de 656 nm, s'entén que hi ha hidrogen a l'atmosfera de l'estrella observada. Mesurant l'espectre d'absorció d'una estrella es pot saber quin tipus d'àtoms conté.
A principis dels anys 1920, no se sabia que hi hagués galàxies. L'univers semblava estar format per un únic conjunt d'objectes estel·lars (el que ara identificam com a Via Làctia); però a l'any 1919, Edwin Hubble mesurà les distàncies a la Terra a Andròmeda i altres nebuloses i descobrí que eren molt més grans que les dels estels menys llunyans de la Via Làctia. D'aquí sorgí la hipòtesis que a l'univers hi havia més galàxies. La història ha anat des de les reticències inicials a acceptar aquest fet fins a l'estimació de que hi ha 125 mil milions de galàxies a partir de les dades de 1999 del telescopi espacial que duu el nom de Hubble..
Edwin Hubble estudià clústers i galàxies que havia identificat. Al 1929 publicà un descobriment de transcendència dins la cosmologia: les freqüències dels colors de la llum dels gasos en aquestes galàxies estaven corregudes cap al vermell. El corriment s'interpretà amb l'efecte Doppler: la lluny de les galàxies llunyanes estava correguda cap a longituds d'ones més llargues (freqüència més baixa), igual que és més greu el so d'un vehicle que s'allunya.
Però això no era tot, com més enfora estava la galàxia, l'efecte Doppler era més pronunciat: la velocitat amb que s'allunyava una galàxia de la Terra era més gran com més enfora estava. Això fou una de les primeres evidències sobre la possible realitat de la teoria del Big Bang per a la formació de l'univers.
En la seva publicació, Hubble presentà un gràfic amb punts {velocitat, distància} i dibuixà la recta que millor els ajustava (Fig. 1), però no hi havia cap model per suposar que hi hagués d'haver algun tipus de relació lineal, ni que els punts s'apartessin de la recta per una qüestió d'error. En tot cas, l'anàlisi de les dades podria posar de manifest si hi havia una correlació entre velocitat i distància (que existeix) i cercar-ne una relació, descobrir el motiu físic pel qual la velocitat depenia de la distància.
El valor del coeficient de correlació lineal està entre –1 i 1
 «
«
Per demostrar que el valor del coeficient de correlació lineal entre unes variables x i y està entre –1 i 1 es pot escriure la definició del coeficient en forma vectorial i usar la desigualtat de Schwarz. En primer lloc, es defineixen
![]()
Amb aquestes noves variables, l'expressió del coeficient de correlació
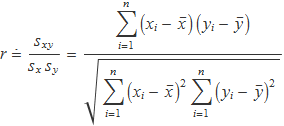
s'escriurà
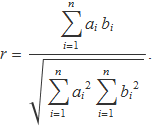
Considerant ai i bi com a les components de dos vectors de n dimensions, a i b, es pot escriure
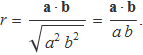
Usant ara la desigualtat de Schwarz, el terme de la dreta tendrà un valor entre -1 i 1, quedant demostrat que el valor de r està acotat:
![]()
El cas |r| =1
 «
«
Aquí es demostra que quan els punts estan exactament sobre una línia recta, el coeficient de correlació lineal val 1 si la recta té pendent positiu i -1 si té pendent negatiu.
Si els punts {xi, yi} estan exactament sobre una línia recta, tots els valors yi es poden calcular a partir dels valors xi. Amb dues constants α i β, es tendrà
yi = α xi + β.
La recta que ajusta els punts, passa pel punt mitjà de les abscisses i les ordenades, llavors
![]()
El coeficient de correlació es pot calcular usant només les abscisses perquè la variable y es pot substituir per x en tots els sumatoris:
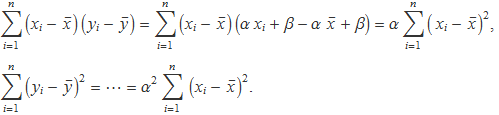
Substituint aquests dos resultats dins l'expressió del coeficient es troba
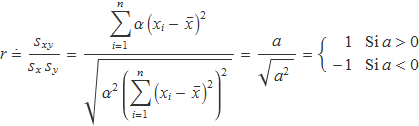
El cas r = 0
 «
«
Perquè el coeficient de correlació lineal doni 0, el numerador ha de ser nul
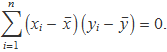
I perquè així passi, hi ha d'haver termes positius i negatius de magnitud semblant en el sumatori. Les variables x i y han de ser independents. El cas està comentat en el tema sobre la covariància.
