
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
covariància i correlació lineal
La covariància
Introducció «
Sigui v una variable que s'ha de calcular a partir de dues altres variables x i y,
v = v(x, y),
(un exemple és l'energia cinètica d'un objecte calculada a partir de la massa i la velocitat).
Si es fan n mesures de les variables x i y, es podran calcular n valors de v. Les dues preguntes que es contesten aquí són quina relació hi ha entre
1) els valors mitjans de x, y i v?
2) les variàncies de x, y i v?
La resposta a la primera pregunta s'usa per respondre la segona i en aquesta segona resposta apareix el sumatori que es denomina covariància de les variables x i y
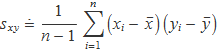
Relació entre els valors mitjans «
Siguin {xi, yi}, i = 1..n, les parelles de valors obtingudes en les mesures. Per a cada parella es pot calcular un valor vi = v(xi, yi). Les mitjanes seran
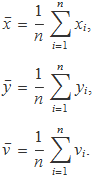
Si la variància de les variables x i y és petita, els valors xi i yi estaran prop dels seus valors mitjans, de manera que la funció v es pot avaluar usant la seva sèrie de Taylor a primer ordre en el punt
P = {x, y}.
L'expressió de la sèrie truncada és
![]()
amb les constants
![]()
![]()
L'expressió aplicada a cada un dels valors vi dóna
![]()
Usant aquests valors aproximats per calcular la mitjana de v es tendrà
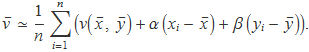
El sumatori es pot separar en tres

El terme del requadre blau és fàcil d'avaluar perquè se suma n vegades un terme constant
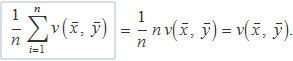
Els sumatoris dels requadres verd i verd vermell donen 0. El càlcul per mostrar-ho és el mateix en els dos sumatoris. S'avaluarà el terme del requadre verd escrivint en gris els termes que no són importants en les operacions:
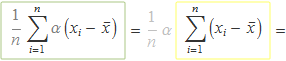
El sumatori en el requadre groc se separa en dos, els quals s'escriuen a continuació en vermell i verd per identificar el resultat de cada un,
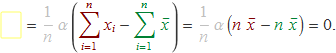
Així s'ha obtingut que el sumatori del terme del requadre verd dóna 0. El requadre vermell és anàleg per a la variable y. Per tant

En conseqüència, la relació entre els tres valors mitjans és
![]()
Relació entre les variàncies. Definició de covariància
 «
«
La variància de la mostra de cada una de les variables és
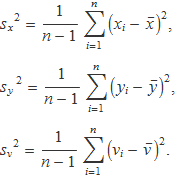
Si la variància de les variables x i y és petita, els valors xi i yi estaran prop dels seus valors mitjans, de manera que la funció v es pot avaluar usant la seva sèrie de Taylor a primer ordre en el punt mitjà. Usarem com a l'apartat anterior
![]()
La variància sv està donada per
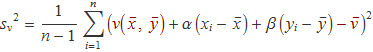
Pel resultat de l'apartat anterior, els termes de color vermell s'anul·len. Elevant al quadrat la suma dels dos termes que queden, separant sumatoris i extraient els factors constants, resulta
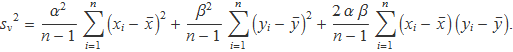
En els dos primers termes surten les variàncies sx i sy, llavors
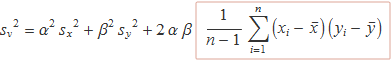
Definint la covariància
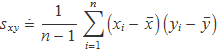
la variància de s es pot escriure, recuperant les definicions d'α i β,
![]()
La covariància de dues variables pot ser negativa perquè el tercer terme de la variància de v pot ser positiu o negatiu segons els signes de la covariància i de les derivades.
Cas de variables independents
 «
«
La covariància de dues variables aleatòries independents tendeix a zero per a un nombre elevat de mesures. El motiu és que quan es resta la mitjana a cada xi queda un nombre de valors negatius semblant al nombre de valors positius. El mateix passa amb l'altra variable. Així, quan es multiplica
![]()
el signe del primer parèntesis serà independent del signe del segon, i quan el producte doni un determinat valor positiu és probable que també surti negatiu i es cancel·lin al sumar-se.
Cada parella de valors {xi, yi} pot representar-se amb un punt d'un pla. La Fig. 1 mostra sèries de 50 mesures d'unes variables amb punts. En uns casos les variables tenen correlació i en altres no. Els punts sense correlació queden distribuïts aleatòriament al voltant del punt mitjà.
Figura 1. Representacions gràfiques de 5 exemples de 50 parelles de valors sense correlació i 5 amb correlació. Les coordenades del punt vermell són les mitjanes de x i y. Dins la figura s'indiquen les variàncies de x i y i la covariància. Explicació en el text.
Exemple d'un càlcul d'errors incorrecte per oblidar la correlació
 «
«
Suposem que una variable física z es calcula com el quocient entre dues quantitats P i Q,
z = P / Q.
La variància de r és
![]()
Es podria donar el cas que les quantitats P i Q es determinin a partir de dues variables mesurades i que una d'aquestes variables o les dues, s'usin per calcular tant P com Q. Llavors,
P = P(x, y),
Q = Q(x, y).
En aquestes circumstàncies P i Q no són variables independents i la variància sz ha d'incloure el terme de la covariància sx,y que tal vegada no sigui menyspreable.
Una alternativa és escriure l'expressió de la variable física z directament en funció de les variables x i y, perquè si són independents tendran una covariància nul·la.
