
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Apèndix
Desigualtat de Cauchy–Schwarz
La desigualtat «
La desigualtat de Cauchy-Schwarz estableix que el producte escalar de dos vectors a i b, de mòduls a i b, compleix
![]()
Dividint els dos membres per (a b)2 i fent l'arrel quadrada es té la cota
![]()
Demostració per a vectors de dimensió 2 (vectors en un pla) «
En el cas de vectors en el pla, la relació s'obté de manera directa perquè
a · b = a b cos(α)
on α és l'angle entre els dos vectors. Com que el valor absolut del cosinus és menor o a igual 1, la desigualtat queda demostrada perquè
![]()
Vectors de n dimensions «
Els productes escalars dels vectors a = {a1 a2 ..., an} i b = {b1 b2 ..., bn} són
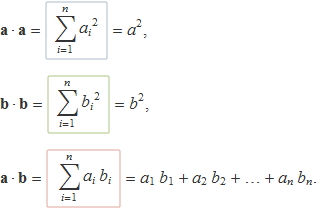
Per fer la demostració de la desigualtat de Cauchy-Schwarz, s'elegeix una suma especial que té tots els termes al quadrat i és, per tant, positiva
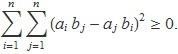
Es desenvolupa el quadrat
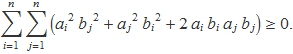
Se separen els sumatoris i s'identifica el valor de cada un,
En la separació dels sumatoris s'usarà l'equivalència
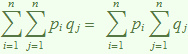
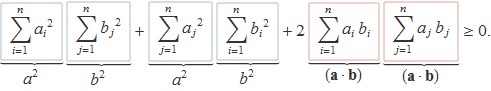
Així es té
![]()
Simplificant el factor 2 i aïllant s'obté la desigualtat de Cauchy-Schwarz,
![]()

