Es demostra en aquest tema que la recta que ajusta un conjunt de punts per mínims quadrats passa pel punt P_m les coordenades del qual són la mitjana de les abscisses i la mitjana de les ordenades dels punts. La Fig. 1 mostra un cas on la simetria dels punts ajustats permet localitzar visualment on està P_m.

El punt P_m s'ha marcat amb el símbol del centre de masses per un símil mecànic: Si en tots els punts hi hagués una bolla igual, llavors P_m seria el centre de masses del conjunt de bolles.

Figura 1. Il·lustració que mostra sis punts i la recta d'ajust. Els punts s'han elegit perquè resulti fàcil identificar els valors mitjans de les abscisses i de les ordenades que localitzen el punt P_m marcat amb el símbol del centre de masses.

Les expressions dels coeficients de la recta y = f(x) = a₁ x + a₀ que ajusta un conjunt de n parelles {x_i y_i} es poden escriure en termes dels valors mitjans;

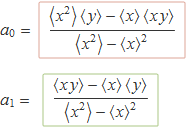
L'ordenada que correspon a la mitjana dels valors x_i és

Substituint els coeficients a₁ i a₀ per les expressions amb les quals es calculen es té

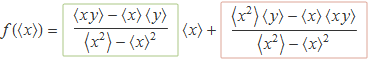
i fent la suma de les fraccions es troba

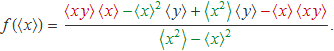
Els dos termes de color vermell es cancel·len, llavors els de color verd es cancel·len amb el denominador i així queda

En conseqüència, la recta que ajusta els punts passa pel punt