Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Ajusts per mínims quadrats
Notacions per expressar els coeficients de la recta d'ajust
Introducció «
Les expressions que donen els coeficients de l'ajust d'una recta per mínims quadrats a un conjunt de n parelles de valors {xi, yi} s'han calculat en el tema de l'ajust lineal i són
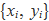
Aquestes expressions es poden escriure de diverses maneres usant notacions distintes.
Σ de sumatori «
Una manera immediata de simplificar la notació és no indicar els índex muts dels sumatoris ni de les variables, de manera que es posa
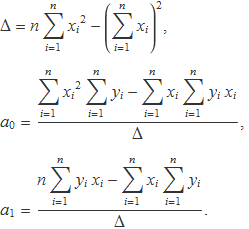
D'aquesta manera les expressions queden més compactes:
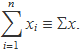
Sx per sumatori de x
 «
«
S'usa
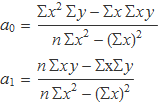
El nombre de valors a sumar no està indicat explícitament, però tanmateix és un valor fix en el càlcul d'un ajust. Les expressions queden en la forma
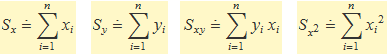
Valors mitjans ![]()
 «
«
El nom d'una variable entre angles indica el valor mitjà d'un conjunt, per exemple
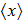
El nombre de termes que inclou ![]() no s'indicarà explícitament per simplificar la notació. La relació de la suma amb el valor mitjà,
no s'indicarà explícitament per simplificar la notació. La relació de la suma amb el valor mitjà,
![]()
es pot aplicar a qualsevol variable, per exemple a les que apareixen a les fórmules que donen els coeficient de l'ajust per mínims quadrats,
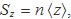
Amb aquesta notació, les expressions que donen els coeficients a0 i a1 de l'ajust y = f(x) = a1 x + a0 es poden escriure en termes dels valors mitjans enlloc dels sumatoris:
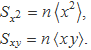
Simplificant, queda
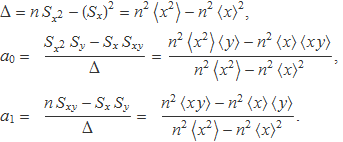
Notació vectorial
 «
«
La notació vectorial resulta més pràctica en altres casos que no en aquest. És útil per demostrar la desigualtat de Cauchy-Schwarz usada en per demostrar la cota del coeficient de correlació lineal.
Els valors del conjunt de n parelles {xi, yi} es poden usar per definir dos vectors de n components
x = {x1, x2, x3, ..., xn},
y = {y1, y2, y3, ..., yn}.
Dos dels sumatoris que apareixen en el càlculs dels coeficients es poden escriure en forma de producte escalar
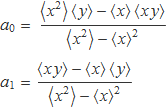
i per a les sumes de components es pot usar
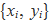
Amb aquesta notació es té
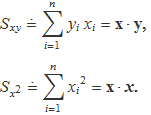
Simplificant, queda