
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Ajusts per mínims quadrats
Ajust amb una recta
Introducció «
Es considera el problema de la determinació dels paràmetres de la recta
f(x) = a1 x + a0
perquè la suma dels quadrats de les separacions entre la recta i un conjunt donat de n punts (xi, yi), i = 1..n, sigui mínima. La suma s'escriurà S(a1, a0) per indicar que depèn dels paràmetres de la recta però no dels punts: les coordenades xi i yi tenen valors fixats. La suma val

Obtenció dels coeficients «
Els valors dels paràmetres a1 i a0 que minimitzen la suma S(a1, a0) és poden obtenir cercant la solució de les equacions

S'ha usat que les derivades parcials d'una funció de dues variables valen zero allà on la funció té un valor local mínim.
Equació de la derivada de S respecte de a1 «
La derivada d'una suma de funcions és la suma de les derivades,
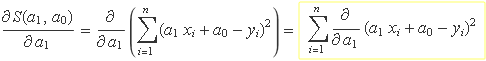
Es deriva el terme al quadrat respecte de a1,
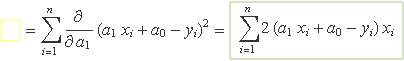
S'usen les propietats dels sumatoris:

S'iguala la derivada a 0
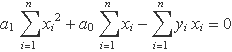
Equació de la derivada de S respecte de a0
 «
«
La derivada d'una suma de funcions és la suma de les derivades,

Es deriva el terme al quadrat respecte de a0
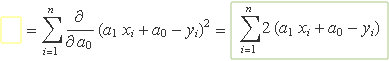
S'usen les propietats dels sumatoris:
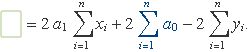
El factor 2 és comú a tots els sumatoris i es podrà eliminar en igualar la derivada a 0. Usant que el tercer sumatori (marcat en blau) és n a0, s'obté l'equació:
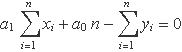
Equacions en forma matricial i solució
 «
«
Les equacions obtingudes en els dos apartats anteriors es poden escriure en forma matricial
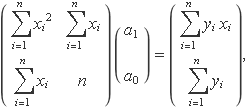
La solució usant la regla de Cramer és
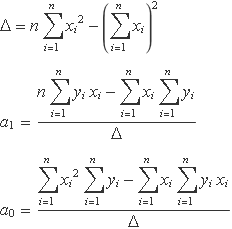
Aquestes solucions es poden escriure de manera compacta de diverses maneres.
