En un tema següent es presentaran les funcions densitat de probabilitat gaussianas definides per dos paràmetres μ i σ, que són la mitjana i la variància poblacional de la variable aleatoris gaussiana considerada. A partir d'una llista de valors L_n d'una variable aleatòria gaussiana se poden cercar els paràmetres de la funció gaussiana de manera que la probabilitat de tenir els valors de la llista sigui màxima. Es troba

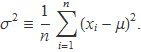
Com que aquests valors es calculen a partir d'una llista, la mitjana i el sumatori dividit per n són estimadors estadístics de la mitjana i la variància poblacional, respectivament.

Definit un estimador estadístic, el primer que s'ha de determinar és si el valor esperat de l'estimador és igual o no al paràmetre corresponent. Si és igual, es dirà que l'estimador no té biaix.

L'estimador estadístic i el concepte de biaix s'introdueixen en aquest tema per justificar perquè la variància de la mostra s_x², com a estimador estadístic de la variància σ² es defineix amb l'expressió

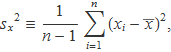
on el sumatori es divideix per n – 1 en lloc de dividir-se per n com es fa amb la variància. Amb aquest canvi de divisor s'aconsegueix que l'estimador tengui el valor esperat igual que la variància poblacional.

Un estimador estadístic és un valor calculat a partir d'una mostra per descriure una propietat desconeguda de la població Ω.

La mitjana d'una mostra és un estimador de la mitjana poblacional. Una propietat θ indeterminada de la població pot tenir més d'un estimador estadístic (cal notar que al canviar la mida de la mostra, l'estimador estrictament ja és diferent). De manera genèrica, l'estimador de la propietat θ_p s'escriu .

Sigui un estimador estadístic d'un paràmetre de valor θ_p d'alguna propietat lligada a una variable aleatòria d'espai mostral Ω. El biaix de l'estimador estadístic és

Si el biaix d'un estimador estadístic és nul, es diu que l'estimador no té biaix.

Es donen a continuació tres estimadors estadístics. El primer i el tercer no tenen biaix, el segon, sí.

La mitjana d'una mostra L_n,

és un estimador estadístic sense biaix de la mitjana poblacional E(X) perquè E(M) = E(X). La demostració ja es va donar a la pàgina sobre valors esperats.

Es considera ara l'estimador estadístic

Tenir una llista de valors L_n = {x₁, x₂, x₃, ..., x_n} és com tenir un valor per a cada una de n variables aleatòries definides amb la mateixa distribució de probabilitat. Llavors,

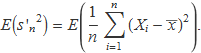
Se suma i resta E(X) = μ:

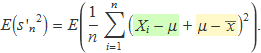
Es desenvolupa el quadrat mantenint els dos termes dels requadres de color agrupats,

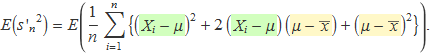
El sumatori de la suma és la suma de sumatoris. S'extreuen els termes que no depenen de l'índex de suma i se sumen els termes que són constants,

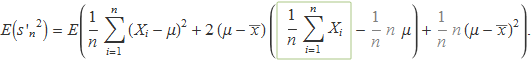
El terme requadrat és , de manera que

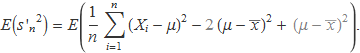
Simplificant termes i usant la linealitat del valor esperat apareix la definició de la variància poblacional (el terme emmarcat de l'expressió següent):

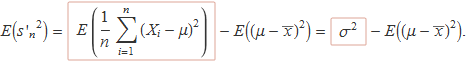
La substitució del resultat dins la definició de biaix d'aquest estimador estadístic per a la variància poblacional,

dóna:

Però

i, per tant, el biaxis val

Es considera ara l'estimador estadístic

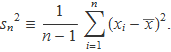
Seguint les primeres passes iguals que abans s'arribarà a

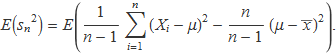
Operant perquè aparegui la definició de la variància poblacional (el terme emmarcat de l'expressió següent) es troba

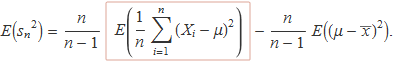
La substitució del resultat i de

dins la definició de biaix de l'estimador estadístic s_n² per a la variància poblacional, s'obté

En conseqüència, s_n² és un estimador estadístic sense biaix de la variància poblacional.