
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Valor esperat de variables aleatòries
Introducció «
El valor esperat d'una variable aleatòria discreta es pot calcular si es coneix la funció de probabilitat. Si la variable és continua, s'ha de conèixer la funció densitat de probabilitat. En cas que no es coneguin les funcions de probabilitat, un estimador sense biaix del valor esperat és el valor mitjà d'una mostra.
Variables aleatòries discretes «
El valor esperat d'una variable aleatòria discreta X amb un espai mostral Ω i una funció de probabilitat PX(ν) és
![]()
Valor esperat dels punts d'un dau «
Sigui X la variable aleatòria igual al número de punts que s'obtenen al llançar un dau. L'espai mostral Ω és {1, 2, 3, 4, 5, 6}. La funció de probabilitat és constant PX(ν) = 1/6, llavors:
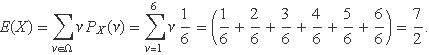
Amb la funció RAN# d'una calculadora es pot simular el llançament d'un dau. Els números aleatoris de la calculadora estan entre 0 i 1. El valor es multiplica per 6, se li suma 1 i es pren la part sencera:
![]()
La repetició d'aquesta operació donarà un conjunt de valors que es podria haver obtingut amb un dau. Si es generen vint valors, s'obtindrà per exemple {1, 5, 5, 1, 5, 6, 3, 3, 5, 3, 4, 1, 5, 3, 3, 2, 6, 6, 1, 1}. La mitjana d'aquests valors és 3.45. Si es generen uns altres vint valors, s'obtendrà un altre conjunt amb una altra mitjana, per exemple 3.3 o 3.7. S'ha de notar que aquestes mitjanes són properes al valor esperat 7/2 = 3.5. E(X) dóna el valor que cal esperar fent una mitjana, és la mitjana que s'obtendrà amb més probabilitat.
Valor esperat de la suma dels punts de dos daus
 «
«
Sigui X la variable aleatòria igual a la suma del número de punts que s'obtenen al llançar dos daus. L'espai mostral Ω és {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. La funció de probabilitat es pot calcular fàcilment. Les cares dels dos daus es poden combinar de 36 maneres diferents, només en 1 cas la suma serà 2 o 12, per tant, PX(2) = PX(12) = 1/36. En 2 casos la suma serà 3 (1+2 i 2+1) i també en dos casos serà 11 (5+6 i 6+5) per tant, PX(3) = PX(11) = 2/36. Es pot construir la taula següent per calcular el valor esperat:
| ν | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | - |
| P(ν) | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 | - |
| ν P(ν) | 2/36 | 6/36 | 12/36 | 20/36 | 30/36 | 42/36 | 40/36 | 36/36 | 30/36 | 22/36 | 12/36 | ΣνP(ν) = 7 |
El valor esperat dels punts d'un dau és 7/2 i el valor esperat de la suma dels punts de dos daus, és el doble. És una casualitat que 2×(7/2) = 7? És el valor esperat de la suma dels punts de tres daus 3×(7/2)? Aviat es donarà la resposta.
Valor esperat de Y = u(X)
 «
«
La variable aleatòria Y = u(X) també és discreta. Aquí se suposarà, per simplificar, que u(x1) ≠ u(x2) si x1 ≠ x2. de manera que la funció u i la inversa u–1 són biunívoques.
El valor esperat de Y és
![]()
Atès que tot valor η s'ha obtingut d'un valor ν amb la funció u, es podrà canviar η per u(ν), PY(η) per PX(u–1(η)) i fer la suma sobre l'espai mostral de X:
![]()
Cas particular. U(X) = c constant
Encara que sembli innecessari remarcar que el valor esperat d'una constant sigui la constant, es pot notar que en l'expressió anterior es té
![]()
de manera que la constant surt fora del sumatori i aquest, per la normalització de la funció de probabilitat, val 1, proporcionant E(c) = c.
Valor esperat d'una combinació lineal de variables aleatòries
 «
«
Siguin X i Y dues variables aleatòries discretes definides sobre els espais mostrals Ω i Ψ respectivament. Siguin a, b dos números reals, ν ∈ Ω i κ ∈ Ψ. El valor esperat de la combinació lineal de les dues variables aleatòries és
![]()
Quan no hi hagi correlació entre les dues variables
![]()
En tal cas,
![]()
El sumatori donarà
![]()
Els dos sumatoris de color blau valen 1 per la normalització de les funcions de probabilitat. Els sumatoris que queden són els valors esperats de X i de Y. per tant:
![]()
Cas E(X + Y)
 «
«
Es tracta del cas a = b = 1 i, directament, es té
E(X + Y) = E(X) + E(Y).
Per exemple, si X i Y són les variables aleatòries corresponents als punts d'un dau llançat a l'atzar, E(X) = E(Y) = 7/2. La variable X + Y és la suma dels punts. A l'exemple 2 es calculà explícitament que E(X + Y) = 7.
Cas E(a X + b Y + c Z + ...)
 «
«
Atès que la suma de dues variables aleatòries és una variable aleatòria, el valor esperat de la suma de tres variables aleatòries es pot trobar aplicant dos pics el resultat obtingut per a la suma de dues variables:
E(a X + b Y + c Z) = E(a X) + E(b Y + c Z) = a E(X) + b E(Y) + c E(Z).
És immediat generalitzar el resultat a la suma d'un nombre qualsevol de variables aleatòries.
![]()
Cas E((X – c)2)
 «
«
Sigui X una variable aleatòria i c una constant. Expandint el quadrat i usant els resultats dels subapartats anteriors resulta:
![]()
En el cas particular que c sigui igual a la mitjana poblacional, μ = E(X), es tendrà
![]()
Simplificant queda
![]()
Aquest cas no se sol poder avaluar en la pràctica perquè μ és desconegut.
Variables aleatòries continues
 «
«
El valor esperat d'una variable aleatòria continua X amb un espai mostral Ω i una densitat de probabilitat PX(x) és
![]()
Valor esperat de Y = u(X)
 «
«
Sigui X una variable aleatòria continua amb densitat de probabilitat PX(x). La variable aleatòria Y = u(X), on u és una funció monòtona, de manera que es pot definir X = u–1(Y), té la densitat de probabilitat tal que
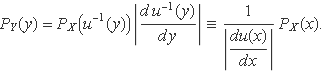
El valor esperat de la variable Y és
![]()
Fent els canvis en cada un dels termes (identificats amb els colors vermell, verd i blau) es té
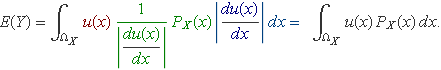
Simplificant queda
![]()
Valor esperat de l'arrel quadrada de la suma de dos números aleatoris entre 0 i 1
 «
«
La funció densitat de probabilitat de la variable aleatòria X igual a la suma de dos números aleatoris entre 0 i 1 és
![]()
El valor esperat de Y es calcularà amb la relació obtinguda com a resultat de l'apartat anterior i directament a partir de la definició.
Càlcul a partir de PX
 «
«
La variable aleatòria Y = u(X) definida amb la funció monòmona
![]()
té la densitat de probabilitat
![]()
Com que la funció densitat de probabilitat està definida amb dues parts, la integral es descompon en dos intervals,
![]()
Càlcul a partir de PY
 «
«
L'univers de la variable aleatòria Y és
![]()
perquè el valor més gran de l'arrel quadrada de la suma dels dos números aleatoris entre 0 i 1 és l'arrel quadrada de 2. Per tant,
![]()
La funció densitat de probabilitat de Y serà, aplicant la definició,
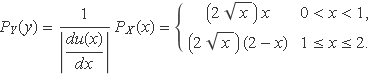
Fent el canvi de variable x per y, s'escriu
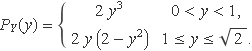
La funció densitat de probbilitat es mostra a la Fig. 1. El valor esperat és,
![]()
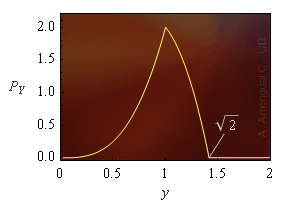
Figura 1. Funció densitat de probabilitat de l'arrel quadrada de la suma de dos números aleatoris dins l'interval [0, 1].
Valor esperat d'una combinació lineal de variables aleatòries
 «
«
Siguin X i Y dues variables aleatòries continues definides sobre els espais mostrals Ω i Ψ respectivament. Siguin a, b dos números reals, x ∈ Ω i y ∈ Ψ. El valor esperat de la combinació lineal de les dues variables aleatòries és
![]()
Quan no hi hagi correlació entre les dues variables
![]()
En tal cas,
![]()
La integral donarà
![]()
Les integrals de color blau valen 1 per la normalització de les funcions densitat de probabilitat. Les integrals que queden són els valors esperats de X i de Y. Per tant,
E(a X + b Y) = a E(X) + b E(Y).
Aquest resultat és el mateix que per a una variable aleatòria discreta. De manera semblant també s'obtenen les relacions:
![]()
![]()
Valor esperat de la mitjana d'una mostra
 «
«
Siguin X i Y dues variables aleatòries amb el mateix espai mostral Ω i igual funció de distribució de probabilitat, els valors esperats de X i Y seran iguals, de manera que
![]()
Aquest resultat es pot generalitzar a n variables aleatòries X1, X2, ..., Xn:
![]()
I, per a una combinació lineal, on tots els coeficients siguin 1/n es tendrà
![]()
Una mostra de n elements de Ω es pot considerar com si fos una mostra de 1 element de cada una de les variables Xi. Quan es calcula la mitjana de la mostra, ![]() , és com calcular un valor de la variable aleatòria
, és com calcular un valor de la variable aleatòria
![]()
Per tant E(M) = E(X): El valor esperat de la mitjana de la mostra és la mitjana poblacional. La mitjana de la mostra és un indicador estadístic sense biaix.
Valor esperat d'una variable amb una funció de probabilitat simètrica
 «
«
Es pot argumentar que el valor esperat d'una variable aleatòria amb una funció de probabilitat simètrica sigui l'abscissa de línia de simetria. A continuació s'escriurà la demostració en el cas d'una variable continua.
Sigui X una variable aleatòria continua amb l'univers
Ω = [c – a, c + a]
de manera que la funció densitat de probabilitat compleix
PX(c – x) = PX(c + x).
El valor esperat de X es determina amb la integral
![]()
Amb el canvi de variable
x = z + c
la integral serà
![]()
on PZ(z) és simètrica respecte a z = 0. La integral serà
![]()
La segona integral dóna zero perquè la funció és imparell i l'interval d'integració simètric respecte de l'origen. Queda així
![]()
