Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Distribució binomial
Propietats de la funció de probabilitat binomial
Introducció «
Si cada una de les persones d'un grup llança n vegades una moneda i compte les cares, s'obtendran resultats diversos. Sigui m el nombre de persones del grup i v(k) el de persones que han obtengut k vegades cara. La mitjana del nombre de cares obtengudes pel grup és
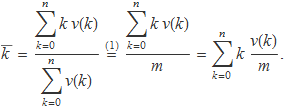
Per escriure la igualtat (1) s'ha tingut en compte que la suma del denominador és igual al nombre de persones del grup. Llavors s'ha entrat m dins el sumatori per fer aparèixer v(k)/m que és la freqüència amb que s'ha obtengut k vegades cara. Aquesta freqüència s'acostarà a la probabilitat d'obtenir k vegades cara si m és suficientment gran. La probabilitat d'obtenir un determinat nombre de cares en n llançaments d'una moneda és pot calcular amb la funció de probabilitat binomial perquè el llançament d'una moneda dóna un resultat aleatori que compleix les condicions d'un procés binomial: i) El resultat de cada llançament és independent dels altres, ii) només hi ha dos resultats possibles (cara ≡ èxit i creu ≡ fracàs) i iii) la probabilitat d'èxit és la mateixa en tots els llançaments, p = 0.5. En conseqüència, com que per a m gran v(k)/m serà aproximadament Bn,p(k), la mitjana de k serà aproximadament la mitjana de la funció de probabilitat binomial
on
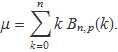
L'expressió 
vol dir estrictament que la probabilitat que la diferència entre la mitjana de k i μ sigui tan petita com es vulgui per a n suficientment gran, és la unitat. Aquesta suposició s'anomena llei dels grans nombres. Hi ha una llei menys restrictiva (llei feble dels grans nombres) la qual estableix que per a qualsevol cota màxima elegida, la probabilitat que la diferència entre la mitjana de k i μ sigui més gran que la cota, és zero per a n suficientment gran. Amb notació matemàtica, cada una d'aquestes lleis es pot escriure així:
(2a) 
A continuació es calcularà la mitjana i la variància de la funció de probabilitat binomial, però primer es comprovarà la normalització d'aquesta funció sumant explícitament les probabilitats Bn,p(k) per a tots els valors de k possibles. El motiu és introduir el mètode de suma que s'aplicarà per determinar la mitjana i la variància. Els resultats que s'obtendran en els tres apartats següents són
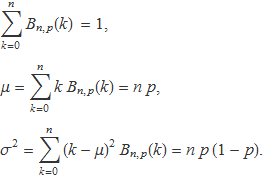
Al final s'esmenta la relació de la funció de probabilitat binomial amb la funció gaussiana, relació que s'analitza amb més detall en un altre tema.
Normalització
«
Per la manera com es defineix, la funció de probabilitat binomial està normalitzada. La suma de tots els valors de Bn,p(k) amb k des de 0 fins a n dóna la unitat. No obstant això, es pot fer la suma explícitament d'una manera fàcil i el càlcul serveix per mostrar el mètode que es farà servir per calcular la mitjana i la variància d'una variable aleatòria binomial.
S'aplica el binomi de Newton
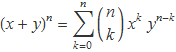
al cas
El terme de l'esquerra és evidentment 1 i el terme de la dreta és precisament la suma de la distribució binomial,
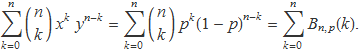
Per tant,
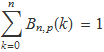
Mitjana
«
La mitjana de la distribució binomial és
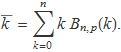
Per avaluar el sumatori, s'usarà el binomi de Newton
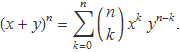
Es deriven els dos membres de la identitat respecte a x,
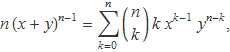
i es multiplica el resultat per x:
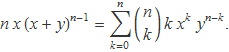
Aquesta identitat s'aplica al cas
El terme esquerra dóna n p i el de la dreta es converteix en el sumatori que dóna la mitjana:
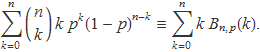
Per tant,
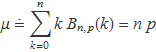
Variància
«
La variància del nombre de cares obtengudes calculada amb la distribució binomial és
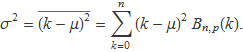
Desenvolupant el quadrat es tendrà
Per determinar el valor mitjà de k2, es pot derivar el binomi de Newton dos pics respecte a x. La primera derivada s'ha fet a l'apartat anterior i la segona derivada dóna
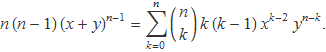
Els dos membres es multipliquen per x2 perquè a la dreta quedi xn:
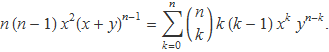
Seguidament, l'expressió s'aplica al cas
per tenir
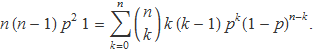
Usant la definició de la funció de probabilitat binomial, es pot escriure
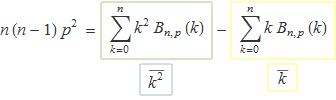
Per tant
Aïllant la mitjana de k2 es té
Així, la variància serà
El resultat es pot escriure usant q = 1 – p,
La desviació estàndard és l'arrel quadrada de la variància.
Relació de la distribució binomial amb la distribució gaussiana
«
Les distribucions de probabilitat binomial i gaussiana són
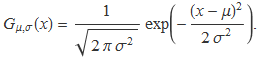
Es compleix que amb
es té
Aquesta relació s'il·lustra a la Fig. 1 i es demostra matemàticament en el tema de la relació de la distribució binomial amb la distribució gaussiana.
Figura 1. Comparació de la distribució binomial amb la gaussiana de les mateixes mitjana i variància, Les distribucions se semblen quan n augmenta.
