
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Distribució normal (gaussiana)
La funció gaussiana com a límit de la funció binomial
Introducció «
Se cerca una expressió límit de la funció densitat de probabilitat (FDP) binomial en el cas n gran. Es demostrarà que

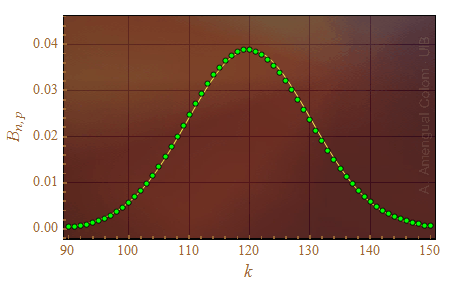
Figura 1. Els punts corresponen a la distribució binomial amb n = 1000 i p = 0.12. La línia groga és la gaussiana de mitjana 120 i variància 105.6.
Les aproximacions usades «
1a) La suma dels n primers números naturals per a n gran,
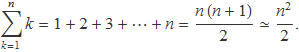
2a) L'aproximació de n! per a n gran (veure apèndix les aproximacions de Stirling),
![]()
3a) La sèrie de Maclaurin per a x ≈ 0 (veure el tema sèries de Taylor),
![]()
Pas 1: El valor de la distribució binomial en funció del valor màxim
 «
«
Considerem l'índex m igual al número sencer més gran inferior a n p:
![]()
Es demostrarà aquí que
![]()
Se cerca el quocient entre dos valors consecutius de Bnp
 «
«
El quocient entre el valor de la distribució binomial per a dos valors consecutius es pot calcular de manera trivial:
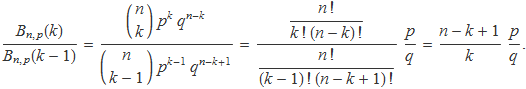
S'aplica el quocient a k = m + i
 «
«
Aplicant el quocient trobat al cas k = m + i resulta
![]()
Canviant el valor de m per n p, usant la definició q = 1 – p i negligint l'1 del numerador s'obté
![]()
Multiplicant i dividint per n, la darrera expressió dóna
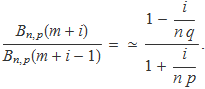
S'aplica el quocient de manera repetida
 «
«
El logaritme del quocient obtingut al final de l'apartat anterior es pot aproximar usant la sèrie de Maclaurin de ln(1 + x) perquè n és gran,
![]()
A partir d'aquesta relació aproximada es pot aïllar
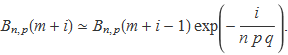
L'aproximació es pot aplicar de manera repetida
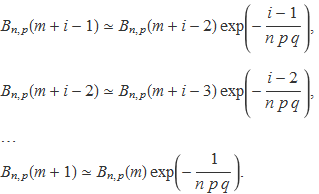
Per tant, considerant que el producte d'exponencials es pot posar com exponencial de la suma d'exponents es tendrà
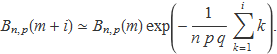
El sumatori es pot aproximar per i2 / 2 de manera que
![]()
Pas 2: Avaluació de Bnp(m)
 «
«
Per a
![]()
es té
![]()
Substituint
![]()
es troba
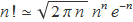
Es canvia
![]()
per obtenir
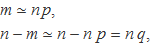
Simplificant termes s'obté directament
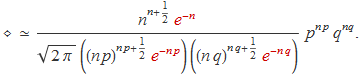
Agrupant resultats
 «
«
Els resultats dels dos apartats anteriors per a ![]() són
són
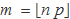
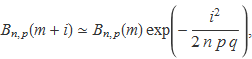
Amb ells es pot escriure
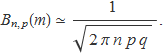
Definint
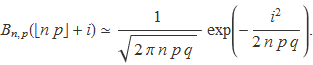
es troba que l'expressió aproximada per a la distribució binomial per a n gran és una gaussiana
![]()
