
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Suma ponderada
El valor més probable és la mitjana ponderada
Introducció
 «
«
En aquest tema s'obté l'expressió de la mitjana ponderada del tema anterior amb un argument probabilístic.
La mitjana ponderada com a valor més probable
 «
«
Considerem dues variables aleatòries gaussianes de mitjana μ i desviacions estàndards σ1 i σ2 respectivament.
La probabilitat que al generar un valor aleatori de la primera variable s'obtengui un valor que s'arrodoneix a x1 és
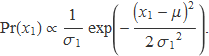
De manera semblant, la probabilitat que al generar un valor per a la segona variable s'obtengui un valor que s'arrodoneix a x2 és
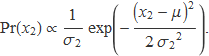
Tots els valors d'un interval petit, per exemple, (0.265, 0.275) s'arrodeixen 0.27. La probabilitat d'obtenir un valor x que s'arrodoneix a 0.27 és igual a la probabilitat que x doni una valor dins l'interval (0.265, 0.275). Si l'interval és petit, la probabilitat és proporcional al valor de la funció gaussiana a x= 0.27.
La probabilitat de generar un valor de cada variable i obtenir x1 per a la primera i x2 per a la segona és el producte de les dues probabilitats anteriors. Usant que el producte de dues exponencials és igual a l'exponencial de la suma dels exponents es té
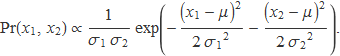
El valor numèric de l'exponencial no es pot calcular sense conèixer μ. Però si x1 i x2 tenguessin el valor μ l'exponent valdria zero, l'exponencial i la probabilitat tendria el valor més gran possible perquè, en qualsevol altre cas, l'exponent seria negatiu, i l'exponencial menor que 1. Per tenir una aproximació del valor de μ se cerca el valor μm que maximitza la probabilitat Pr(x1, x2). La probabilitat que els valors de x1 i x2 estiguin a prop del valor central és més gran que la probabilitat que estiguin enfora, de manera que cercant el valor de μm es tendrà generalment una bona aproximació de μ. L'equació que dóna μm és l'habitual per cercar els extrems d'una funció,
![]()
Feta la derivada, s'obté
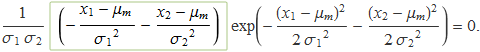
L'únic terme que es pot anul·lar és el que està dins el requadre i s'anul·la quan
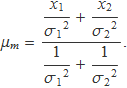
El resultat es pot escriure igual que en el tema anterior,
![]()
amb
![]()
Prendre com a estimador de μ el valor que fa màxima la probabilitat d'haver obtingut uns valors particulars en un mostreig també es fa en altres situacions, per exemple per obtenir una estimació dels paràmetres d'una distribució gaussiana a partir d'una mostra de valors. Aquí s'han considerat dos conjunts de mostres de dues distribucions gaussianes de variància diferent i allà es té una mostra de valors d'una distribució gaussiana.
