
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Suma ponderada
Suma ponderada de variables aleatòries gaussianes
Introducció
 «
«
En aquest tema es descriu com trobar la mitjana i la variància d'un conjunt de valors C d'una variable aleatòria gaussiana a partir de les mitjanes i les variàncies de dos subconjunts complementaris A i B.
Primer es mostrarà el càlcul de la mitjana de C com una mitjana ponderada de les mitjanes dels subconjunts amb pesos determinats pels errors estàndard. Després es mostrarà el càlcul de l'error estàndard de C.
La generalització dels càlculs quan C es descompongui en més de dos subconjunts és immediata.
La importància pràctica dels resultats mostrats aquí és que l'error estàndard és la desviació estàndard de la funció de distribució de les mitjanes i l'error estàndard es pren usualment com la incertesa de la mitjana d'un conjunt de mesures experimentals obtingudes en presència d'errors aleatoris. Es tendrà un procediment per combinar diversos valors amb incerteses de la mateixa magnitud en un únic resultat.
Es demostrarà que diversos resultats xa ± sa, xb ± sb, ..., xz ± sc per a la mateixa magnitud física x es poden combinar amb un únic resultat. Definint els pesos wk com els inversos de les variàncies, sk-2, es tendrà
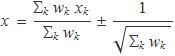
La mitjana ponderada de dues mitjanes
 «
«
Sigui X una variable aleatòria de mitjana μ i desviació estàndard σ i siguin A i B dos conjunts de n i m valors aleatoris d'aquesta variable:
A = {a1, a2, ..., an},
B = {b1, b2, ..., bm}.
Les mitjanes d'aquests conjunts de valors són
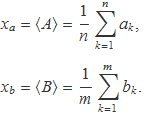
En lloc d'usar l'expressió de la desviació estàndard d'una mostra per després calcular els errors estàndard de les mostres A i B, s'usarà ara que les desviacions estàndard de les mostres són properes a σ si n és gran de manera que els errors estàndard de les mostres A i B seran aproximadament
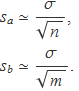
Com que els valors dels conjunts A i B corresponen a la mateixa variable aleatòria, es podrien considerar elements d'una mostra de n + m elements:
C = A ∪ B = {a1, a2, ..., an, b1, b2, ..., bm}.
La mitjana d'aquesta mostra és
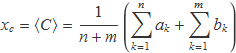
i l'error estàndard, atès que ara hi ha m + n valors, serà aproximadament
![]()
A continuació se cerquen expressions per calcular xc i sc en funció de xa, xb, sa i sb.
Per simplificar la forma de les expressions finals, es definiran els pesos wb = sb–2 i wb = sb–2.
Càlcul de la mitjana ponderada
 «
«
La mitjana xc es pot obtenir a partir de les mitjanes xa i xb de manera immediata amb l'expressió
![]()
Perquè surtin els errors sa i sb en lloc de n i m, s'inverteixen les definicions de l'error estàndard i es tendrà
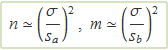
Així l'expressió de la mitjana es pot escriure
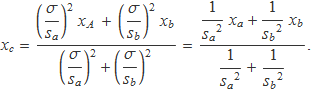
Aquesta expressió per a xc és una mitjana ponderada de xa i xb amb els pesos
![]()
Amb els pesos, s'escriu
![]()
Càlcul de la incertesa de la mitjana ponderada com un error propagat
 «
«
L'expressió que s'acaba d'obtenir per calcular xc també serveix per calcular la incertesa sobre aquesta mitjana.
El valor de xc és una combinació lineal de xa i xb i l'error propagat es calcula de manera immediata tenint en compte que els errors estàndard sa i sb donen la incertesa sobre xa i xb,
![]()
Considerant que xc és una funció de xa i xb,
![]()
s'aplicarà l'expressió general per a la propagació de la incertesa per variables aleatòries independents
![]()
Les derivades donen
![]()
Usant la relació de les incerteses amb els pesos, queda
![]()
Per tant,
![]()
Càlcul de la incertesa de la mitjana ponderada com un error estàndard
 «
«
L'error estàndard sc és
![]()
Perquè en aquesta expressió surtin els errors sa i sb en lloc de n i m, s'inverteixen les definicions de l'error estàndard. S'usarà com ja s'ha fet per calcular la mitjana
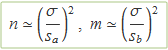
i s'escriurà
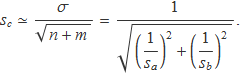
Aquesta relació dóna
![]()
i, usant les definicions dels pesos, es pot escriure:
![]()
Aquesta expressió coincideix amb l'obtinguda a l'apartat anterior.
Cas particular: La mitjana ponderada de dues mesures de la mateixa incertesa
 «
«
Es considera en aquest apartat el cas de dos conjunts de valors de la variable aleatòria gaussiana X amb el mateix nombre n d'elements,
A = {a1, a2, ..., an},
B = {b1, b2, ..., bn}.
Per a la mitjana s'obté de manera immediata
![]()
Aquest resultat equival a calcular directament la mitjana del conjunt
C = A ∪ B = {a1, a2, ..., an, b1, b2, ..., bn}.
Pel que fa a l'error estàndard, es té
![]()
De manera que
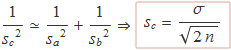
Aquest resultat és el que correspon a l'error estàndard de 2n valors, que és el nombre d'elements d'A i B junts.
Cas general: La mitjana ponderada de més de dues mitjanes
 «
«
Els resultats obtinguts per als conjunts A i B es poden estendre a un nombre indefinit de conjunts de valors d'una variable aleatòria X de mitjana μ i desviació estàndard σ.
El pes de cada conjunt es calcula d'acord amb el seu error estàndard
wi = si-2.
La mitjana de x es pot calcular a partir de la mitjana de cada conjunt
![]()
i l'error estàndard del conjunt es pot calcular a partir dels errors estàndards de cada conjunt
![]()
