Descripció funcions dels botons »

Imaginem una màquina com la de la figura que genera i guarda sense mostrar un número internament quan es posa en marxa i cada pic que es pitja el botó SET. La màquina simula el llançament de cert nombre de daus blaus i el mateix nombre de daus vermells en pitjar el botó RAN#; els punts dels daus blaus se sumen al número ocult i els dels daus vermells es resten; llavors, la màquina mostra per pantalla el resultat. Com que el llançament dels daus és un procés aleatori, els números que dóna la màquina són també aleatoris. Pitja el botó ON i el botó  RAN# unes quantes vegades per veure com es generen alguns números.

Considerarem dues mitjanes. La primera és la mitjana de n números generats per la màquina al pitjar RAN#. La segona és la mitjana de m mitjanes de n números generats per la màquina.

La primera mitjana per a n = 100 la dóna la màquina pitjant el botó S/100. El botó SIGMA dóna la desviació estàndard d'aquest cent números.

La segona mitjana es podria obtenir pitjant m vegades la tecla S/100, anotant els valors i calculant la mitjana.  

Encara que la màquina no mostra el número ocult, en els apartats següents se suposarà que l'hem extret i se sap que és 279.

Quan es fa una mesura d'una magnitud física, els errors aleatoris provoquen que el valor obtingut sigui distint del valor real amb una discrepància depenent dels tipus d'errors. El valor de la magnitud física és com el número ocult de la màquina i el valor obtingut afectat pels errors aleatoris és com el valor que mostra la màquina per pantalla.

Amb els dos tipus de mitjanes, es mostrarà que la variància dels números generats és més gran que la variància de les mitjanes.

Quan el que interessa és la mitjana, es donarà la desviació estàndard de la distribució de les mitjanes com a mesura de l'error. Aquesta desviació és la que determina la incertesa sobre el valor de la mitjana.

Addicionalment, la variància de la distribució de les mitjanes s'intentarà estimar a partir del càlcul d'una única mitjana.

Es comença a pitjar repetidament el botó RAN# i es van anotant els valors que dóna la màquina:

287, 285, 271, 280, 277, 285, 275, 279, ...

L'operació es repeteix n = 100 vegades. Amb la llista de valors es genera un histograma, el qual es mostra a la Figura 1. La mitjana d'aquesta seqüència de valors és

Mitjana = 278.7

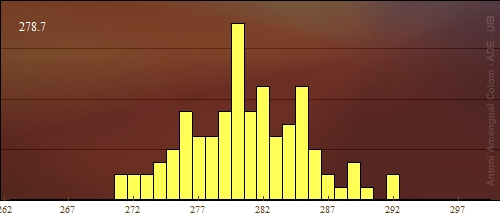
Figura 1. Histograma de 100 valors obtinguts amb la màquina.

Una nova seqüència de cent valors generada amb la màquina serà diferent, i tendrà una mitjana i un histograma distints. A la Fig. 2 es mostren els histogrames de vint-i-quatre seqüències de cent valors amb mitjanes

280.21, 279.2, 279.4, 278.94, 278.96, 280.07, ...

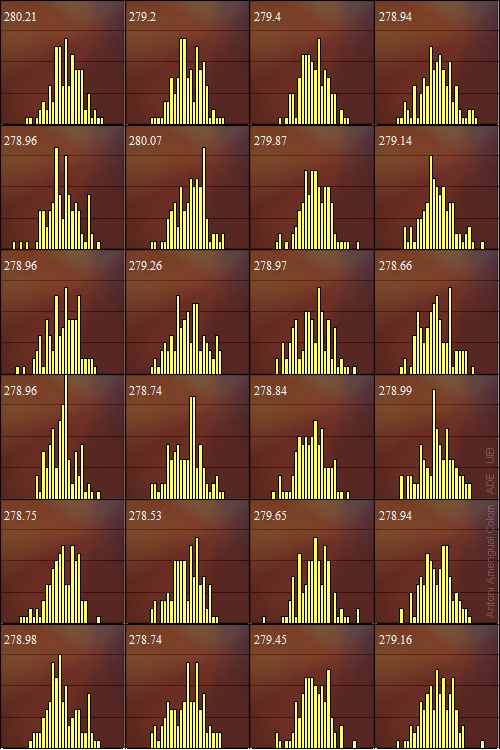
Figura 2. Vint-i-quatre histogrames de igual nombre de sèries de 100 valors obtinguts amb la màquina.

A la Fig. 3 es mostra l'histograma de les mitjanes de m seqüències de 100 valors. Es pot posar el cursor sobre la figura per ampliar-la horitzontalment, però el que s'ha de tenir present especialment és que el domini de la figura sense ampliar s'ha fet igual que el dels histogrames de les figures 1 i 2. Resulta molt evident que l'histograma de les mitjanes és més estret que l'histograma del valors d'una seqüència.

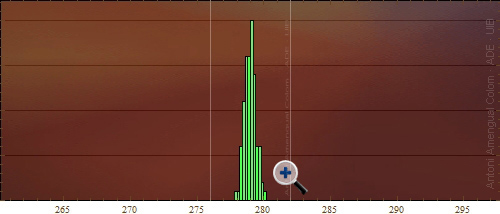
Figura 3. Histograma dels valors de les mitjanes d'un conjunt de sèries de 100 valors.

Siguin X i Y dues variables aleatòries gaussianes amb la mateixa mitjana μ i la mateixa variància σ. Quina és el valor esperat i la desviació estàndard de la variable aleatòria Z = (X + Y)/2?

S'avança a continuació com obtenir la resposta. El procediment es demostrarà en el tema següent sobre la propagació dels errors aleatoris.

Si un valor z de la nova variable aleatòria es calcula amb una funció f(x, y) es té

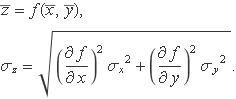
Per a f(x, y) = (x + y)/2, resulta

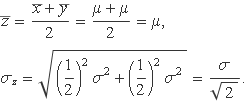
De manera semblant però més general per a n variables aleatòries amb la mateixa mitjana μ i la mateixa variància σ, el valor aleatori  

té el valor esperat

i la desviació estàndard

Quan les n variables aleatòries corresponen a la mateixa quantitat, σ_z es denomina error estàndard i és la desviació estàndard de la mitjana de n valors de la mateixa quantitat.

A la Fig. 4 es mostren dos histogrames per a 100 valors d'una variable aleatòria gaussiana x de mitjana pròxima a 25 i desviació estàndard al voltant de 0.1.

Figura 4. Histogrames per a dos conjunts de 100 valors de la mateixa variable aleatòria. Les línies verdes acoten el domini μ ± σ.

L'histograma de les mitjanes de 200 conjunts de 100 valors de la variable aleatòria té una desviació estàndard més petita. En aquest cas, es redueix en un factor 10 (10 és l'arrel del nombre de valors de cada conjunt).

Figura 5. Histograma de 200 mitjanes.

Per a una variable z calculada a partir de x amb una funció f(x) es tendrà

L'error estàndard de z es calcularà multiplicant la derivada per l'error estàndard de x. La Fig. 6 mostra un exemple per a la funció f(x) = π/x (s'ha posat π per acostar la mitjana de z a la de x i poder fer un gràfic únic).

Els histogrames verd i vermell mostren el que s'ha comentat: La desviació estàndard de la funció de probabilitat de les mitjanes d'una variable és més petita que la desviació estàndard de la mateixa funció per a la variable.

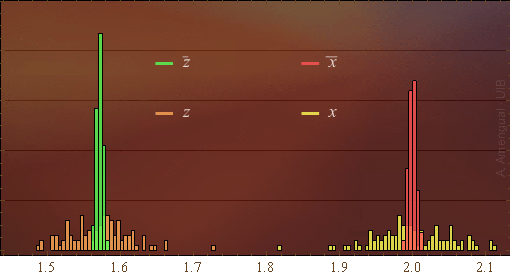
Figura 6. Histograma de 200 mitjanes.

Una persona A podria haver obtingut per a un conjunt de n = 100 valors de x,

x_A =  2.003 ± 0.050 = 2.00 ± 0.05.

La incertesa aquí és la desviació estàndard i s'expressa primer amb dues xifres decimals per comparar-la amb altres valors. Calculant els n valors de z = π/x, s'obté

z_A =  1.569 ± 0.039 = 1.57 ± 0.04.

La desviació estàndard del conjunt de valors de z dóna el mateix que amb la propagació de l'error

Una altra persona B que obtingués un altre conjunt de 100 valors, obtendria altres resultats. Per exemple;

x_B =  1.995 ± 0.050 = 2.00 ± 0.05,

z_B =  1.575 ± 0.040 = 1.58 ± 0.04.

(la mitjana dóna 1.5754, per això és 1.575 amb tres decimals i 1.58 amb dos decimals. Sense saber el valor amb 4 decimals no es podria decidir si s'ha d'escriure 1.58 o 1.57).

Usant la desviació estàndard, les persones A i B donarien els resultats

z_A = 1.57 ± 0.04,

z_B = 1.58 ± 0.04.

La discrepància entre els dos resultats no és significativa. De fet, la diferència entre els valors centrals és de només 0.01, en front de la desviació estàndard 0.04, un valor quatre vegades més gran. Les persones A i B poden donar el valor mitjà que han calculat amb l'error estàndard en lloc de la desviació estàndard. Amb n = 100, l'error estàndard és la desviació estàndard dividida per 10, llavors, els resultats s'expressarien d'aquesta manera:

z_A = 1.569 ± 0.004,

z_B = 1.575 ± 0.004.

La discrepància entre els dos resultats segueix sense ser significativa. L'error estàndard reflecteix bé la incertesa sobre el valor de la mitjana de z.