
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Ajusts per mínims quadrats
Per què es minimitza la suma de distàncies al quadrat?
Introducció «
S'ha considerat el problema de la determinació dels paràmetres a1 i a0 de la recta
f(x) = a1 x + a0
perquè la suma dels quadrats de les separacions entre la recta i un conjunt de n parelles de valors (xi, yi), i = 1..n,
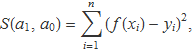
sigui mínima. La qüestió considerada en aquest tema és per què s'ha triat la suma dels quadrats. La suma dels valors absoluts,
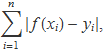
o de les potències parells més grans que dos,
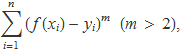
també donen una mesura acumulada de valors positius per quantificar la distància entre els punts i una recta. Si bé l'ús d'una potència en lloc del valor absolut simplifica l'avaluació de la derivada de la suma i prendre m igual 2 correspon a usar la potència més baixa possible, la justificació de perquè la distància entre els punts i la recta es posa al quadrat sorgeix quan el problema s'analitza suposant que els valors de les variables yi tenen un error aleatori amb distribució gaussiana.
Càlcul de la probabilitat
 «
«
Suposem que entre dues variables x i y existeix la relació
y = f(x) = a1 x + a0
amb unes constant a1 i a0 desconegudes. Per a diversos valors x = xi es pot fer una mesura per determinar el valor de la variable y. El valor mesurat tendrà sempre una incertesa. Se suposarà que la mesura de la variable y per a x = xi és un mostreig d'una distribució gaussiana de mitjana f(xi) i variància σy2.
La probabilitat que es mesuri el valor y = yi ± σy per a x = xi és proporcional a
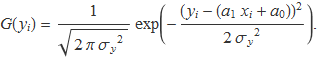
Si es fan n mesures per a un conjunt de valors {x1, x2, ..., xn}, la probabilitat d'obtenir un conjunt de valors {y1, y2, ..., yn} serà proporcional al producte de les probabilitats. Com que el producte d'exponencials és igual a l'exponencial de la suma dels exponents, la probabilitat serà proporcional a
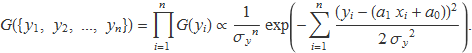
Càlcul dels paràmetres a1 i a0
 «
«
La probabilitat G({y1, y2, ..., yn}) no es pot avaluar numèricament perquè a1, a0 i σy no tenen valors coneguts, però s'establirà el següent:
Els valors dels paràmetres a1 i a0 que s'usaran per definir la relació lineal entre les variables y i x seran els que facin més probable haver obtingut la sèrie de valors {y1, ..., yn}.
Per tant, cal cercar el màxim de G resolent les equacions
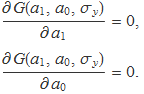
Aquí s'ha usat que les derivades parcials d'una funció valen zero allà on la funció té un valor local extrem.
A l'expressió de G hi surt el paràmetre σy que també és desconegut i se suposarà que el seu valor també maximitza la funció. Per tant, també es té la tercera condició
![]()
Ara bé, aquesta condició no és necessària per fixar els valors dels paràmetres a1 i a0.
Com que σy és constant, es té
![]()
I com que S(a1, a0) és positiu, l'exponencial serà màxima per als valors a1 i a0 que minimitzin S. Els valors dels paràmetres a1 i a0 són la solució de les equacions següents en les quals σy no hi apareix:

Aquestes dues equacions són les mateixes que s'establiren en el tema anterior cercant la recta que minimitzava la suma de les distàncies verticals al quadrat entre la recta i els punts. Les dues equacions són lineals i donen els valors dels dos paràmetres estimats per mínims quadrats.
Càlcul de la variància
 «
«
La tercera condició
![]()
es pot escriure de la manera següent per realitzar la derivada:
![]()
Així resulta fàcil veure que s'obté
![]()
L'expressió només es pot anul·lar si
![]()
és a dir
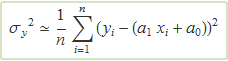
No s'ha posat el símbol igual perquè l'expressió de la dreta dóna un estimador estadístic de la variància i no el valor de la variància.
La semblança d'aquesta expressió amb l'expressió de la variància d'una mostra és notable. El problema d'usar una d'aquestes expressions com a estimador estadístic és que dóna un valor esbiaixat.
Es va demostrar en aquest apartat del tema Estimador estadístic i biaix que l'estimador estadístic sense biaix de la variància d'una variable aleatòria calculada a partir d'una mostra, s'obtenia canviat el divisor n per n – 1. Aquí l'estimador estadístic sense biaix de σy resulta ser
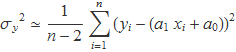
La demostració d'aquesta expressió no es fa en aquest curs, però cal indicar que la divisió per n – 2 en lloc de per n està relacionada amb el fet que a1 i a0 són dos paràmetres que no es coneixen exactament per a la població i s'han de calcular a partir dels valors de la mostra. L'estimador de la variància s'ha de calcular a partir de la mostra, però en l'expressió per calcular l'estimador hi figuren dos paràmetres, a1 i a0, que ja s'han hagut de calculat a partir de la mostra.
