Una vegada analitzada la propagació de l'error amb operacions bàsiques, s'ha d'analitzar la propagació amb funcions elementals d'una variable.

En els casos següents, u(x) representa una funció de la variable x, la qual té un valor x₀ i una incertesa δ_x.

Els resultats presentats aquí es poden deduir d'una altra manera com es mostrarà en el tema de la propagació de l'error per funcions d'una variable.

Es vol determinar la incertesa de

u(x) = x²

per a x = x₀ ± δ_x. Aquesta incertesa es pot trobar usant l'expressió de l'error del producte obtinguda en el tema anterior per a p ≡ u i a = b = x. Es tendrà

u₀ = u(x₀) = x₀²,

Aïllant, resulta

La incertesa de l'arrel quadrada d'una variable z positiva es pot calcular amb el resultat de l'apartat anterior aplicada a

Es tendrà

Aïllant la incertesa que se cerca s'obté

Exemple »

Es vol determinar la incertesa de

u(x) = xⁿ

per a x = x₀ ± δ_x i n un número sencer més gran que 1. El cas n = 2 ja està resolt en el primer apartat, quan s'ha considerat el quadrat de x. Aquí serà un cas particular. La funció s'escriurà

u(x) = xⁿ = x xⁿ⁻¹

Usant el resultat final de la incertesa relativa del producte de dues variables es tendrà

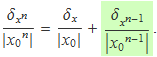
Aquesta expressió és vàlida per a qualsevol valor de n. Aplicada a n – 1 dóna

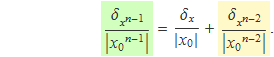
Aplicada a n – 2 dóna

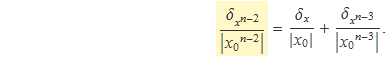
Aplicant l'expressió repetidament fins a n – (n – 1), es tendran igualtats que combinades donen

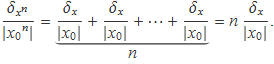
Aïllant la incertesa, es té

expressió vàlida per a n ≥ 2.