La funció gamma, que s'identifica amb la lletra grega d'aquest nom en majúscula, es pot definir de maneres diferents. Aquí es consideraran dues definicions: el límit d'Euler i la integral d'Euler. La primera és vàlida per a variables reals i complexes. La segona només és vàlida si la part real de la variable complexa és positiva.

Dues propietats fonamentals de la funció gamma són el valor que té per a z = 1,

Γ(1) = 1,

i la relació de recurrència

Γ(z + 1) = z Γ(z).

Aplicant aquesta darrera relació de manera repetida després de prendre z igual a un nombre sencer positiu  n fins que surti Γ(1) a la dreta, es troba

Γ(n + 1) = n!

Per aquesta igualtat, la funció gamma es considera una extensió del factorial d'un número sencer positiu als números reals i complexos.

El límit d'Euler és

Com resulta evident mirant el denominador, la funció gamma divergeix a z = 0 i a z igual a qualsevol sencer negatiu. A la Fig. 1 es mostra una representació de la funció gamma per a z igual a un número real x.

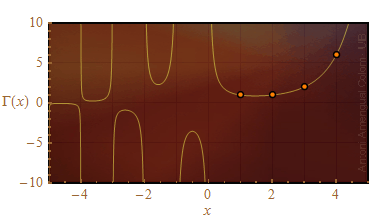
Figura 1. Representació de la funció gamma per a x real. Els punts taronja marquen el valor de la funció gamma per a x igual a 1, 2, 3 i 4. El mínim a la part positiva de les abscisses és Γ(1.46) = 0.886.

De manera particular i directa a partir de la definició resulta

Per demostrar que es compleix la relació de recurrència, s'aplica la definició a la variable z + 1:

El darrer terme de color verd es posa com n^z per n, llavors es multiplica i divideix per z i s'agrupen termes. Així queda

Finalment, s'usa la relació

per obtenir

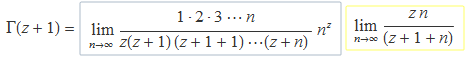
El primer terme és Γ(z), el segon val z i el producte dóna la relació de recurrència.

La funció gamma per a variables complexes amb la part real positiva es pot definir amb la integral d'Euler

De manera particular i directa a partir de la definició resulta

Per demostrar que es compleix la relació de recurrència, s'aplica la definició a la variable z + 1:

i es fa una integració per parts,

Per demostrar l'equivalència de la integral d'Euler en el domini d'existència amb el límit d'Euler es comença per definir

Es mostrarà a continuació que segons com es calculi

s'obté la integral o el límit d'Euler i com que el límit és únic, l'equivalència entre les dues definicions quedarà demostrada.

Per calcular el límit es té en compte que el límit de la integral és igual a la integral del límit (aquest fet s'hauria de demostrar) i la definició del número e,

A la integral que defineix Γ(z, n) es fa el canvi de variable

t = n u

i s'integra succesivament per parts. Amb el canvi de variable es té

S'integra per parts. La part integrada s'anul·la en els límit 0 i 1 i queda

Es repeteix la integració per parts i s'obté

La repetició successiva de la integració per parts n vegades dóna

La integral ara és immediata i s'obté finalment

La definició de Γ(z) era el límit per a n → ∞ d'aquesta expressió,

Queda així demostrat que el límit dóna Γ(z) en la forma de límit d'Euler com aquí o d'integral d'Euler com a l'apartat anterior. Per tant, les definicions són equivalents en el domini de z tal que la part real de z és positiva.

S'ha de distingir si n és parell o imparell.

Els valors de la funció gamma per als semienters n/2 es calculen directament amb el factorial si n es parell. Escrivint n = 2k, amb k un número natural, es té

Γ(n/2) = Γ(k) = (k – 1)!

S'ha de partir de

Llavors, es pot aplicar la relació de recurrència per calcular els valors de la funció gamma per a semienters més grans. Per exemple,

A la Taula 1 es recullen els valors de Γ(n/2) per a n imparells des de 1 fins a 15.

Taula 1. Valors de la funció gamma per als primers valors de n / 2 amb n imparell.