
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Distribució de Poisson
Relació amb la funció de probabilitat exponencial
Introducció «
La funció de probabilitat de Poisson
![]()
s'ha presentat com un cas límit de la funció de probabilitat binomial. La probabilitat de tenir k èxits en un nombre molt gran n de proves quan la probabilitat d'èxit p és molt petita, està donada per la funció de probabilitat de Poisson Pμ(k) amb μ = n p. El nombre de proves n i la probabilitat p deixen de ser paràmetres explícits de la funció. De fet, a la pràctica només es coneix el valor esperat de k que és μ. En la definició tampoc apareix cap referència a un temps durant el qual es fan les n proves.
S'ha esmentat el temps per introduir-lo com a variable en el problema que es presenta. Suposem que n és el nombre de proves que es fan en un interval de temps τ. La funció de probabilitat de Poisson dóna la probabilitat que es donin k èxits en el temps τ. Quina funció de densitat de probabilitat PΔ(t) dóna la probabilitat que l'interval temporal Δ entre dos èxits tengui un determinat valor t ≤ τ? La resposta és la funció densitat de probabilitat exponencial
PΔ(t) = λ e–λt
amb λ = μ/τ. La distribució de probabilitat corresponent és
FΔ(t) ≡ Pr(Δ ≤ t) = 1 – e–λt.
Propietats de la distribució exponencial
 «
«
La distribució de probabilitat, el valor esperat, la variància i la desviació estàndard de la funció de probabilitat exponencial es calcularan a continuació a partir de la densitat de probabilitat
PΔ(t) = λ e–λt, t ∈ [0, ∞)
L'exponencial està multiplica per λ perquè la funció de probabilitat estigui normalitzada.
Els resultats seran
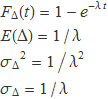
Distribució de probabilitat
 «
«
La distribució de probabilitat exponencial es calcula amb la integral
![]()
La integració de l'exponencial és immediata i dóna
![]()
Valor esperat
 «
«
Variància
 «
«
La variància és
![]()
El desenvolupament del parèntesis al quadrat dóna tres termes i el resultat després d'integrar cada un d'ells és
Integrals »
![]()
Desviació estàndard
 «
«
La desviació estàndard de la distribució exponencial és
![]()
Relació entre la distribució de Poisson i la distribució exponencial
 «
«
Considerem un fenomen que dóna resultats numerables i ordenats en el temps que es qualifiquen d'èxit de manera que la densitat de probabilitat que el temps entre dos èxits consecutius sigui t està donada per la funció exponencial
PΔ(t) = λ e–λt.
L'origen de temps es pot prendre en qualsevol moment (un fet que es pot demostrar matemàticament). Llavors, les probabilitats dels èxits següents es concreten de manera trivial. .
1) La probabilitat que un èxit es doni en un temps entre t i t + dt és igual a la funció densitat de probabilitat multiplicada per dt.
2) La probabilitat que un èxit es doni abans de l'instant t està donada per la distribució de probabilitat directament.
3) La probabilitat que un èxit es doni en un temps posterior a l'instant t és 1 menys la probabilitat del cas anterior.
Aquestes tres probabilitats es recullen en el requadre següent:
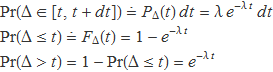
A continuació es calcularan les probabilitats que el nombre d'èxits durant un interval τ de durada fixada sigui k = 0, 1, 2 i 3, i es demostrarà que aquestes probabilitats són iguals a Pμ(k) amb μ = λ τ. Una demostració completa s'hauria de fer per incloure qualsevol nombre d'èxits.
Cap èxit
 «
«
Cercar la probabilitat que des d'un temps zero fins el temps τ no es doni cap èxit és equivalent a cercar la probabilitat que l'interval Δ entre dos èxits sigui més gran que τ. La justificació es pot donar considerant que si no s'havia donat un èxit fins a t = 0, la probabilitat que es doni al cap d'un interval Δ després de t = 0 és la mateixa que amb un origen de temps anterior. Per tant,
Pr(cap èxit durant interval τ) = Pr(Δ > τ) = 1 – e–λτ.
La probabilitat Pr(Δ > τ) es calcularà a partir de la del succés complementari
Pr(Δ > τ) = 1 – Pr(Δ ≤ τ).
En aquesta expressió, Pr(Δ ≤ τ) és la funció distribució de probabilitat. Per tant,
Pr(Δ > τ) = 1 – FΔ(τ) = 1 – (1 – e–λτ) = e–λτ.
Aquesta probabilitat és la mateixa que l'obtenguda amb la funció de probabilitat de Poisson per a k = 0 i μ = λ τ.
![]()
1 èxit dins un interval de durada α i el cas α = τ
 «
«
Cercar la probabilitat que des d'un temps zero fins el temps α es doni exactament 1 èxit és equivalent a cercar la probabilitat que es doni 1 èxit en el moment t ∈ [u, u + du] per a qualsevol u ∈ [0, α] i que no se'n doni cap dins l'interval Δ = α – u posterior:
![]()
![]()
![]()
La probabilitat que des de zero a τ es doni només 1 èxit es calcula amb l'expressió que s'acaba d'obtenir amb α = τ,
![]()
Aquesta probabilitat coincideix amb Pμ(1) amb μ = λ τ.
2 èxits dins un interval de durada α i el cas α = τ
 «
«
La probabilitat que des de zero a α es donin exactament 2 èxits és igual a la probabilitat que es doni 1 èxit dins un interval de durada Δ1 = v ≤ α i exactament un altre a l'interval Δ2 = α – Δ1

El terme del segon requadre és, aplicant el resultat de l'apartat anterior,
![]()
La probabilitat dels dos èxits serà per tant
![]()
La integració és immediata i dóna

La probabilitat que des de zero a α = τ es donin 2 èxits exactament es calcula amb l'expressió que s'acaba d'obtenir amb α = τ,

Aquesta probabilitat coincideix amb Pμ(2) amb μ = λ τ.
3 èxits dins un interval de durada α i el cas α = τ
 «
«
La probabilitat que des de zero a α es donin exactament 3 èxits és igual a la probabilitat que es donin 2 èxits dins un interval de durada Δ1 = v ≤ α i exactament un altre a l'interval Δ2 = α – Δ1
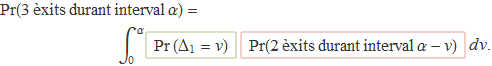
El terme del segon requadre és, aplicant el resultat de l'apartat anterior,
![]()
La probabilitat dels tres èxits serà per tant
![]()
La integració és immediata i dóna

La probabilitat que des de zero a α = τ es donin 3 èxits exactament està donada per l'expressió que s'acaba d'obtenir amb α = τ,

Aquesta probabilitat coincideix amb Pμ(3) amb μ = λ τ.
