
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Distribució de Poisson
La funció de Poisson com a límit de la funció binomial
Introducció «
La funció densitat de probabilitat de Poisson es deduirà com a límit de la funció de probabilitat binomial.
La probabilitat de tenir k èxits en n proves quan la probabilitat d'èxit és p està donada per
![]()
L'avaluació del número binomial es fa impossible quan n és un número molt gran. La funció no es pot calcular exactament, però si p té un valor petit es pot trobar una aproximació. Aquí se cercarà l'expressió límit de la distribució binomial de mitjana μ = n p quan n és molt gran i la probabilitat p = 1/μ, molt petita. Es trobarà que la funció de probabilitat binomial en aquest límit dóna la funció de probabilitat de Poisson,
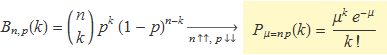
Aproximació del número binomial per a n gran «
Per definició, el número binomial és
![]()
Per a n gran, es pot usar l'aproximació de Stirling
![]()
Per a valors de k propers al valor esperat de k, n – k també és un número molt gran i
![]()
Amb l'aproximació dels factorials, el número binomial serà
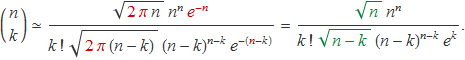
Els termes escrits en vermell es cancel·len. Després, els dos termes marcats en verd es poden negligir perquè el seu quocient tendeix a 1 quan n augmenta (d'altra banda també són negligibles al costat dels termes que estan a la dreta de cada un). Així s'obté
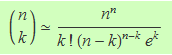
Recordant la definició del número e
 «
«
El número e es defineix com un límit:
![]()
Per calcular
![]()
la constant a es passa dividint el denominador i es fa el canvi n = a m:
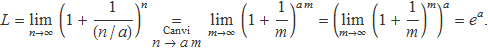
D'altra banda, per a k constant, positiu o negatiu, també es té
![]()
perquè n + k = n.
Aproximació de la funció de probabilitat binomial per a n gran
 «
«
L'expressió de la distribució binomial amb
![]()
i l'aproximació del número binomial per a n gran permeten escriure una expressió aproximada per calcular la funció de probabilitat binomial Bn,p(k). Es té
![]()
Els termes escrits en vermell, s'agrupen de la manera següent
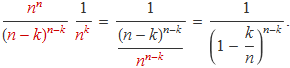
Amb aquesta agrupació es té
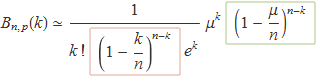
Els dos termes dins requadres es poden aproximar per a n gran pels seus valors en el límit n → ∞. Usant el resultat de l'apartat anterior per a a = –k i a = –μ els valors en el límit són e–k i e–μ, respectivament. Així

Les exponencials del denominador es cancel·len i s'arriba a l'aproximació
![]()
L'expressió de la dreta és la funció de probabilitat de Poisson:
![]()
