Curs ADE: Definicio

Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.

Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.

Test khi quadrat

Definició i propietats de la funció densitat de probabilitat khi quadrat

Introducció «

La funció densitat de probabilitat de la suma de m variables aleatòries gaussianes de mitjana zero i variància unitat s'anomena funció densitat de probabilitat khi quadrat per a m graus de llibertat.

El nom prové de la lletra grega khi, χ. La notació per a la funció és senzillament χ², sense fer explícit el nombre de graus de llibertat.

La lletra khi s'usa en aquest context sempre escrita al quadrat. Dins l'Electromagnetisme, la lletra χ s'usa per identificar les susceptibilitats elèctrica i magnètica, les constants que caracteritzen la resposta d'un material quan està en un camp elèctric o magnètic extern. En aquest context, se sol escriure amb els subíndex e i m.

Definició «

Siguin Y_i, i = 1..m, un conjunt de m variables aleatòries gaussianes independents de mitjana 0 i variància 1.

Sigui X_m la variable aleatòria definida com a suma dels quadrats d'aquestes m variables Y_i,

X_m = Y₁² + Y₂² + ... + Y_m².

La funció densitat de probabilitat de cada una de les variables Y_i és gaussiana. Per la seva banda, la funció densitat de probabilitat de la suma X_m és

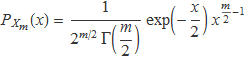
"ade_1.gif"

on Γ(m/2) és el valor de la funció gamma per al semienter m/2.

Propietats «

Es donen a continuació el valor esperat i la variància de la variable aleatòria X_m.

Valor esperat «

El valor esperat de X_m és

El resultat de la integració dóna

E(X_m) = m

Variància «

La variància de X és

El resultat de la integració dóna

V(X_m) = 2m

Gràfics i taules «

Es donen a continuació taules i gràfics per a diferents graus de llibertat de les funcions densitat de probabilitat P_{X_m}(x) i distribució de probabilitat F_{X_m}(x).

Gràfics de la funció densitat de probabilitat per a m graus de llibertat «

Es presenten les funcions densitat de probabilitat per a les variables X₁, X₂ i X_m amb m ≥ 3.

m = 1 «

La funció densitat de probabilitat de la variable definida positiva

X₁ = Y₁²

és

la qual divergeix a l'origen i decreix monòtonament cap a zero. X₁ és senzillament el quadrat d'una variable aleatòria gaussiana.

m = 2 «

La funció densitat de probabilitat de la variable definida positiva

X₁ = Y₁² + Y₂²

és

la qual val 0.5 a l'origen i decreix monòtonament cap a zero.

m ≥ 3 «

Les formes de les funcions densitat de probabilitat per a les variables X_m amb m ≥ 3, es mostren a la Fig. 1a. Les funcions valen 0 a l'origen, tenen un màxim i tendeixen a 0 per a x → ∞. La posició del màxim està més a la dreta com més gran és m. Posar x/m a l'eix d'abscisses (m és el nombre de graus de llibertat però també és el valor esperat de la variable aleatòria X_m) permet acostar les posicions dels màxims a la Fig. 1b.

Els fulls de càlcul tenen la funció DISTR.CHI(χ²; m) que dóna el valor de la funció densitat de probabilitat khi quadrat per a m graus de llibertat.

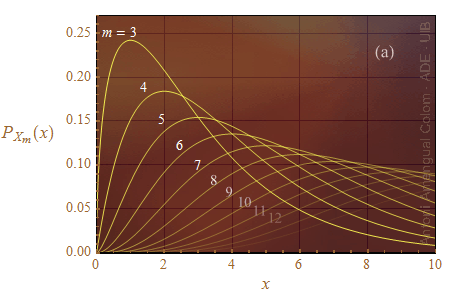
"ade_6.gif"

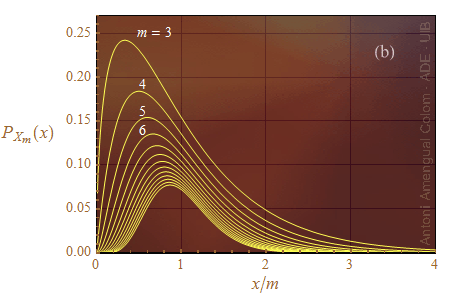
"ade_7.gif"

Figura 1. a) Funcions densitat de probabilitat per a diferents graus de llibertat a partir de tres. b) Les mateixes funcions dibuixades amb l'eix d'abscisses escalat segons el nombre de graus de llibertat que és també el valor esperat de la variable aleatòria.

Gràfics de la distribució de probabilitat per a m graus de llibertat «

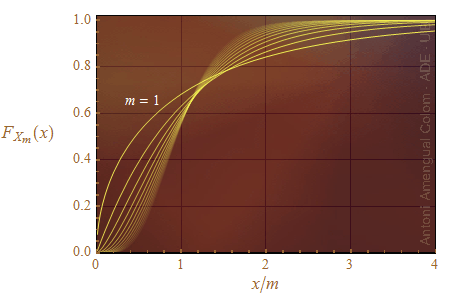
"ade_8.gif"

Figura 2. Distribucions de probabilitat per a diferents graus de llibertat amb l'eix d'abscisses escalat segons el valor esperat m.

La distribució de probabilitat es calcula amb la integral

Les corbes de les distribucions de probabilitat per a m des de 1 fins a 12 es mostren a la Fig. 2.

Taules i gràfics de la probabilitat que khi quadrat sigui més gran que un valor donat «

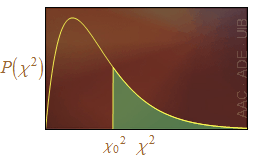
"ade_10.gif"

Figura 3. L'àrea de color verd dóna la probabilitat que khi quadrat sigui més gran que el valor khi zero quadrat.

Per analitzar si l'histograma d'un conjunt de dades és compatible amb una determinada distribució de probabilitat teòrica, s'usa la probabilitat que χ² sigui més gran que un valor donat χ₀². Tal probabilitat està representada per l'àrea de color verd a la Fig. 3. Aquesta probabilitat,

es calcula amb la integral

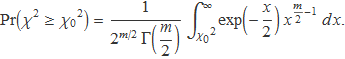
"ade_12.gif"

Les probabilitats en tant per cent per a diferents graus de llibertat se solen donar en forma de taula com les incloses a continuació per a conjunts des d'un grau de llibertat fins a 30 (marcau sobre » per desplegar les taules).

Taules de probabilitats »

Taules de la probabilitat que χ² sigui més gran que χ₀² segons el nombre de graus de llibertat m. S'ha de notar que les entrades a la primera columna són per a χ²/m.

Graus de llibertat de 1 a 10 »

$\frac{χ^{2}}{m}$	m=1	2	3	4	5	6	7	8	9	10
0.0	100	100	100	100	100	100	100	100	100	100
0.1	75.2	90.5	96.0	98.2	99.2	99.6	99.8	99.9	100.0	100.0
0.2	65.5	81.9	89.6	93.8	96.3	97.7	98.6	99.1	99.4	99.6
0.3	58.4	74.1	82.5	87.8	91.3	93.7	95.4	96.6	97.5	98.1
0.4	52.7	67.0	75.3	80.9	84.9	87.9	90.3	92.1	93.6	94.7
0.5	48.0	60.7	68.2	73.6	77.6	80.9	83.5	85.7	87.6	89.1
0.6	43.9	54.9	61.5	66.3	70.0	73.1	75.6	77.9	79.8	81.5
0.7	40.3	49.7	55.2	59.2	62.3	65.0	67.2	69.2	71.0	72.5
0.8	37.1	44.9	49.4	52.5	54.9	57.0	58.7	60.3	61.6	62.9
0.9	34.3	40.7	44.0	46.3	48.0	49.4	50.5	51.5	52.4	53.2
1.0	31.7	36.8	39.2	40.6	41.6	42.3	42.9	43.3	43.7	44.0
1.1	29.4	33.3	34.8	35.5	35.8	35.9	36.0	35.9	35.9	35.8
1.2	27.3	30.1	30.8	30.8	30.6	30.3	29.9	29.4	29.0	28.5
1.3	25.4	27.3	27.2	26.7	26.1	25.3	24.6	23.8	23.1	22.4
1.4	23.7	24.7	24.1	23.1	22.1	21.0	20.0	19.1	18.2	17.3
1.5	22.1	22.3	21.2	19.9	18.6	17.4	16.2	15.1	14.1	13.2
1.6	20.6	20.2	18.7	17.1	15.6	14.3	13.0	11.9	10.9	9.96
1.7	19.2	18.3	16.5	14.7	13.1	11.6	10.4	9.28	8.30	7.44
1.8	18.0	16.5	14.5	12.6	10.9	9.48	8.25	7.19	6.28	5.50
1.9	16.8	15.0	12.7	10.7	9.07	7.68	6.51	5.54	4.72	4.03
2.0	15.7	13.5	11.2	9.16	7.52	6.20	5.12	4.24	3.52	2.93
2.1	14.7	12.2	9.79	7.80	6.22	4.98	4.00	3.23	2.61	2.11
2.2	13.8	11.1	8.58	6.63	5.14	4.00	3.12	2.44	1.92	1.51
2.3	12.9	10.0	7.52	5.63	4.23	3.20	2.42	1.84	1.41	1.07
2.4	12.1	9.07	6.58	4.77	3.48	2.55	1.87	1.38	1.02	0.76
2.5	11.4	8.21	5.76	4.04	2.85	2.03	1.44	1.03	0.74	0.53
2.6	10.7	7.43	5.03	3.42	2.34	1.61	1.11	0.77	0.54	0.37
2.7	10.0	6.72	4.40	2.89	1.91	1.27	0.85	0.57	0.39	0.26
2.8	9.43	6.08	3.84	2.44	1.56	1.00	0.65	0.42	0.28	0.18
2.9	8.86	5.50	3.36	2.06	1.27	0.79	0.50	0.31	0.20	0.12
3.0	8.33	4.98	2.93	1.74	1.04	0.62	0.38	0.23	0.14	0.09
3.1	7.83	4.50	2.56	1.46	0.84	0.49	0.29	0.17	0.10	0.06
3.2	7.36	4.08	2.23	1.23	0.68	0.38	0.22	0.12	0.07	0.04
3.3	6.93	3.69	1.94	1.03	0.56	0.30	0.16	0.09	0.05	0.03
3.4	6.52	3.34	1.69	0.87	0.45	0.23	0.12	0.07	0.03	0.02
3.5	6.14	3.02	1.48	0.73	0.36	0.18	0.09	0.05	0.02	0.01
3.6	5.78	2.73	1.29	0.61	0.29	0.14	0.07	0.03	0.02	0
3.7	5.44	2.47	1.12	0.51	0.24	0.11	0.05	0.02	0.01	0
3.8	5.13	2.24	0.97	0.43	0.19	0.09	0.04	0.02	0	0
3.9	4.83	2.02	0.85	0.36	0.16	0.07	0.03	0.01	0	0
4.0	4.55	1.83	0.74	0.30	0.12	0.05	0.02	0	0	0
4.1	4.29	1.66	0.64	0.25	0.10	0.04	0.02	0	0	0
4.2	4.04	1.50	0.56	0.21	0.08	0.03	0.01	0	0	0
4.3	3.81	1.36	0.49	0.18	0.07	0.02	0	0	0	0
4.4	3.59	1.23	0.42	0.15	0.05	0.02	0	0	0	0
4.5	3.39	1.11	0.37	0.12	0.04	0.01	0	0	0	0
4.6	3.20	1.01	0.32	0.10	0.03	0.01	0	0	0	0
4.7	3.02	0.91	0.28	0.09	0.03	0	0	0	0	0
4.8	2.85	0.82	0.24	0.07	0.02	0	0	0	0	0
4.9	2.69	0.74	0.21	0.06	0.02	0	0	0	0	0
5.0	2.53	0.67	0.18	0.05	0.01	0	0	0	0	0
5.1	2.39	0.61	0.16	0.04	0.01	0	0	0	0	0
5.2	2.26	0.55	0.14	0.03	0	0	0	0	0	0
5.3	2.13	0.50	0.12	0.03	0	0	0	0	0	0
5.4	2.01	0.45	0.10	0.02	0	0	0	0	0	0
5.5	1.90	0.41	0.09	0.02	0	0	0	0	0	0
5.6	1.80	0.37	0.08	0.02	0	0	0	0	0	0
5.7	1.70	0.33	0.07	0.01	0	0	0	0	0	0
5.8	1.60	0.30	0.06	0.01	0	0	0	0	0	0
5.9	1.51	0.27	0.05	0	0	0	0	0	0	0
6.0	1.43	0.25	0.04	0	0	0	0	0	0	0
6.1	1.35	0.22	0.04	0	0	0	0	0	0	0
6.2	1.28	0.20	0.03	0	0	0	0	0	0	0
6.3	1.21	0.18	0.03	0	0	0	0	0	0	0
6.4	1.14	0.17	0.02	0	0	0	0	0	0	0
6.5	1.08	0.15	0.02	0	0	0	0	0	0	0
6.6	1.02	0.14	0.02	0	0	0	0	0	0	0
6.7	0.96	0.12	0.02	0	0	0	0	0	0	0

Graus de llibertat de 11 a 20 »

$\frac{χ^{2}}{m}$	m=11	12	13	14	15	16	17	18	19	20
0.0	100	100	100	100	100	100	100	100	100	100
0.1	100	100	100	100	100	100	100	100	100	100
0.2	99.8	99.8	99.9	99.9	100.0	100.0	100.0	100.0	100	100
0.3	98.6	99.0	99.2	99.4	99.6	99.7	99.7	99.8	99.9	99.9
0.4	95.7	96.4	97.1	97.6	98.0	98.3	98.6	98.8	99.0	99.2
0.5	90.5	91.6	92.6	93.5	94.2	94.9	95.5	96.0	96.4	96.8
0.6	83.0	84.4	85.6	86.7	87.8	88.7	89.5	90.3	91.0	91.6
0.7	74.0	75.3	76.5	77.7	78.7	79.7	80.6	81.5	82.3	83.0
0.8	64.0	65.1	66.1	67.0	67.9	68.7	69.5	70.3	71.0	71.7
0.9	53.9	54.6	55.2	55.8	56.4	56.9	57.4	57.9	58.3	58.7
1.0	44.3	44.6	44.8	45.0	45.1	45.3	45.4	45.6	45.7	45.8
1.1	35.6	35.5	35.3	35.1	35.0	34.8	34.6	34.4	34.2	34.1
1.2	28.0	27.6	27.1	26.7	26.3	25.8	25.4	25.0	24.6	24.2
1.3	21.7	21.0	20.4	19.8	19.2	18.6	18.1	17.6	17.1	16.6
1.4	16.5	15.7	15.0	14.3	13.7	13.1	12.5	12.0	11.4	10.9
1.5	12.4	11.6	10.8	10.2	9.53	8.95	8.41	7.90	7.43	6.99
1.6	9.13	8.38	7.70	7.08	6.51	5.99	5.52	5.09	4.69	4.33
1.7	6.67	5.99	5.38	4.84	4.36	3.93	3.55	3.20	2.89	2.61
1.8	4.82	4.23	3.71	3.26	2.87	2.53	2.23	1.97	1.74	1.54
1.9	3.44	2.95	2.53	2.17	1.86	1.60	1.38	1.19	1.03	0.89
2.0	2.44	2.03	1.70	1.42	1.19	1.00	0.84	0.71	0.59	0.50
2.1	1.71	1.39	1.13	0.92	0.75	0.61	0.50	0.41	0.34	0.28
2.2	1.19	0.94	0.75	0.59	0.47	0.37	0.30	0.24	0.19	0.15
2.3	0.82	0.63	0.49	0.38	0.29	0.22	0.17	0.13	0.10	0.08

Graus de llibertat de 21 a 30 »

$\frac{χ^{2}}{m}$	m=21	22	23	24	25	26	27	28	29	30
0.0	100	100	100	100	100	100	100	100	100	100
0.1	100	100	100	100	100	100	100	100	100	100
0.2	100	100	100	100	100	100	100	100	100	100
0.3	99.9	99.9	100.0	100.0	100.0	100.0	100.0	100.0	100	100
0.4	99.3	99.4	99.5	99.6	99.7	99.7	99.8	99.8	99.8	99.9
0.5	97.2	97.5	97.7	98.0	98.2	98.4	98.6	98.7	98.9	99.0
0.6	92.2	92.7	93.2	93.7	94.1	94.5	94.9	95.2	95.6	95.9
0.7	83.8	84.5	85.1	85.7	86.3	86.8	87.4	87.9	88.3	88.8
0.8	72.3	72.9	73.5	74.1	74.7	75.2	75.7	76.2	76.7	77.2
0.9	59.2	59.6	59.9	60.3	60.7	61.0	61.4	61.7	62.0	62.3
1.0	45.9	46.0	46.1	46.2	46.2	46.3	46.4	46.4	46.5	46.6
1.1	33.9	33.7	33.5	33.3	33.1	33.0	32.8	32.6	32.4	32.3
1.2	23.9	23.5	23.1	22.8	22.4	22.1	21.8	21.4	21.1	20.8
1.3	16.1	15.7	15.2	14.8	14.4	14.0	13.6	13.3	12.9	12.6
1.4	10.5	10.0	9.61	9.20	8.82	8.46	8.11	7.78	7.46	7.16
1.5	6.57	6.19	5.83	5.49	5.17	4.88	4.60	4.34	4.09	3.86
1.6	4.00	3.69	3.41	3.15	2.92	2.70	2.50	2.31	2.14	1.98
1.7	2.36	2.14	1.93	1.75	1.59	1.44	1.30	1.18	1.07	0.97
1.8	1.36	1.20	1.07	0.94	0.84	0.74	0.66	0.58	0.52	0.46
1.9	0.76	0.66	0.57	0.49	0.43	0.37	0.32	0.28	0.24	0.21

La informació de les taules per a un conjunt de punts seleccionats es presenten sobre les representacions gràfiques a la figura 3.

Figura 4. Probabilitat que χ-quadrat sigui més gran que un valor donat segons el nombre de graus de llibertat m = g.

Taules dels valors de probabilitat 5 % i 1 % «

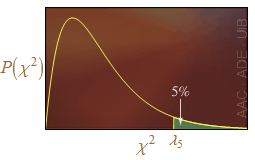
Quan no sigui necessari conèixer el valor exacte de la probabilitat

sinó que basti saber si és més gran que el 5 % o l'1 %, és suficient comparar χ² amb els valors λ₅ i λ₁ per als quals

Pr(χ² ≥ λ₅) = 0.05,

Pr(χ² ≥ λ₁) = 0.01.

Els valors de λ₅ i λ₁ s'usaran per determinar si la discrepància entre els valors observats en un histograma i els esperats és significativa o molt significativa, respectivament.

"ade_14.gif"

$m$	1	2	3	4	5	6	7	8	9	10
$λ_{5}$	3.84	5.99	7.81	9.49	11.1	12.6	14.1	15.5	16.9	18.3
$λ_{1}$	6.63	9.21	11.3	13.3	15.1	16.8	18.5	20.1	21.7	23.2
$m$	11	12	13	14	15	16	17	18	19	20
$λ_{5}$	19.7	21.0	22.4	23.7	25.0	26.3	27.6	28.9	30.1	31.4
$λ_{1}$	24.7	26.2	27.7	29.1	30.6	32.0	33.4	34.8	36.2	37.6
$m$	21	22	23	24	25	26	27	28	29	30
$λ_{5}$	32.7	33.9	35.2	36.4	37.7	38.9	40.1	41.3	42.6	43.8
$λ_{1}$	38.9	40.3	41.6	43.	44.3	45.6	47.0	48.3	49.6	50.9
$m$	31	32	33	34	35	36	37	38	39	40
$λ_{5}$	45.0	46.2	47.4	48.6	49.8	51.0	52.2	53.4	54.6	55.8
$λ_{1}$	52.2	53.5	54.8	56.1	57.3	58.6	59.9	61.2	62.4	63.7

Taula 1. Valors de les variables λ₅ i λ₁ definides en el text en funció del nombre de graus de llibertat.