El trucatge d'un dau carregant-lo de manera exagerada quedarà en evidència després de pocs llançaments, però si la càrrega només afavoreix una mica l'obtenció d'unes cares, la trampa pot passar desapercebuda. Qui jugui sèries llargues amb el dau trucat podrà obtenir avantatge si ho sap (la banca?), però qui només jugui algunes tirades, no es veurà segurament perjudicat. De fet, un dau legal pot donar sèries que pareixin obtingudes amb un dau trucat.

La qüestió tractada en aquest tema és decidir si un dau cúbic és legal analitzant els resultats d'una sèrie de llançaments.

Un dau cúbic és legal si mostra qualsevol cara a la part superior amb igual probabilitat quan es llança sobre una taula.

Encara que un dau sigui legal, ningú no espera que al llançar-lo sis vegades, surti una cara diferent cada vegada. És més, la probabilitat que en sis llançaments no es repeteixi cap cara és molt baixa, 5!/6⁵ = 0.015.

Els histogrames del nombre de vegades que han sortit les cares d'un dau en dues sèries de 300 llançaments es mostren a la Fig. 2. El valor esperat, 300/6 = 50 per a cada cara, s'ha marcat amb una línia verda.

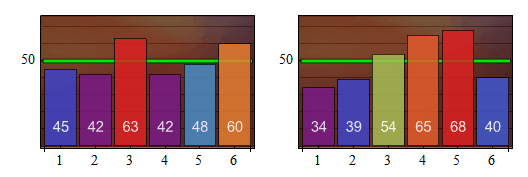
Figura 1. Els números de color blanc són els nombres de vegades que han sortit les cares 1 a 6 en una seqüència simulada de 300 llançaments d'un dau. La línia verda marca el valor esperat d'un dau legal.

Per quantificar globalment la discrepància entre els valors observats en una sèrie i el valor esperat, es calcularà la suma

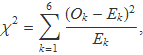
on O_k és el nombre de vegades que ha sortit la cara k i E_k és el valor esperat, en aquest cas 50 per a totes les cares.

En aquest punt, χ² és el nom pel sumatori, però encara no s'ha mostrat que el resultat d'aquest sumatori tengui la distribució de probabilitat khi quadrat. Al final d'aquests apartats, es veurà que és així, però per ara només és el nom del sumatori.

La sèrie de l'histograma de la Fig. 1 esquerra dóna

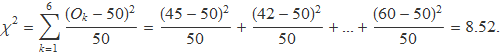
La sèrie de l'histograma de la dreta dóna

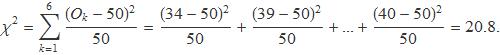
La primera sèrie ha quedat més a prop dels valors esperats, però es necessita algun element addicional per tenir una idea concreta del que signifiquen els valors 8.52 i 20.8.

La simulació del llançament de daus és senzilla, basta generar números aleatoris sencers entre 1 i 6, ambdós inclosos. Simular l'obtenció de 10000 sèries de 300 llançaments i calcular χ² per a cada una és pot fer ràpidament amb un ordenador. A la Fig. 2 es mostra un histograma dels valors obtinguts de χ². Els valors entre entre 3 i 3.5 són els que s'han repetit més.

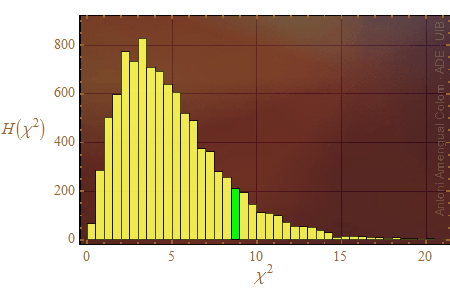
Figura 2. Histograma dels valors de khi quadrat de 10000 sèries de 300 llançaments cada una.

Aquest histograma de H(χ²) permet analitzar les característiques d'un dau posat a prova en una sèrie de 300 llançaments.

La sèrie que ha donat χ² = 8.52 cau dins la classe del rectangle dibuixat de color verd a la Fig. 2. De les deu mil sèries de la simulació, 210 han donat un valor dins aquesta classe. Les classes amb χ² < 8.5 sumen 8723 casos, de manera que més de 1200 casos han donat per damunt de 8.5. En termes de probabilitat es pot dir que

Pr(χ² ≥ 8.5) ≈ 13 %.

Per la seva banda, la sèrie que ha donat χ² = 20.8 cau dins una classe que queda en el límit dret de la Fig. 2. No arriba a distingir-se una barra, només s'aprecia una petita retxa negra que parteix de la marca 20. Només onze sèries de les deu mil han donat un valor més gran que 20.8. Es pot dir en termes de probabilitat que

Pr(χ² ≥ 20.5) ≈ 0.12 %.

La sèrie de l'histograma de l'esquerra de la Fig. 1 s'aconseguí amb la primera simulació, però la de l'histograma de la dreta es va haver de cercar. És molt poc probable obtenir una sèrie amb χ² per damunt de 20.

Els dos histogrames de la Fig. 1 mostren l'ús del càlcul de χ² d'una sèrie de 300 llançaments per decidir si el dau és legal o no amb determinada probabilitat. Si s'obté χ² = χ₀², es considerarà que la discrepància entre el nombre de cares obtingudes i les esperades és

significativa si

molt significativa si

Naturalment, en el dos casos es pensarà que el dau pot estar trucat. Quan la discrepància s'ha de qualificar de molt significativa, la probabilitat que el dau estigui realment trucat és més gran. La sèrie obtinguda és molt poc probable que s'hagi obtingut amb un dau legal.

Un dau legal es podria usar en una sèrie de 300 llançaments i donar χ² = 20, però és tan poc probable quan es fa una única sèrie, que el dau es dóna per trucat.

El nombre de vegades que surt una cara concreta d'un dau cúbic en una sèrie de 300 llançaments no és 50 sempre. Fixant l'atenció en la cara de 5 punts en una simulació de 10000 sèries de 300 llançaments, la cara surt exactament 50 vegades en només 644 sèries, en totes les altres surten valors més petits o més grans (molt pocs pics per baix de 30 o per damunt de 70).

La probabilitat d'obtenir O_k vegades la cara de k punts en 300 llançaments es calcula amb la funció de probabilitat binomial amb n = 300 i p = 1/6 (la probabilitat de tenir èxit —que surti la cara elegida— és 1/6). Els punts de color verd de la Fig. 3 corresponen a

H(O_k) = 10000 B_1/6,300(O_k).

A la mateixa Fig. 3 s'hi presenta l'histograma del nombre de sèries on la cara de 5 punts ha sortit O₅ vegades. Com es d'esperar, la discrepància entre els valors obtinguts i esperats és insignificant.

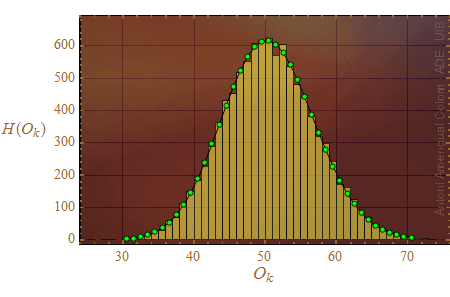
Figura 3. Histograma del nombre de vegades que surt la cara de 5 punts en 300 llançaments en una simulació de 10000 sèries. Els punts verds són els valors esperats calculats amb la funció de probabilitat binomial i són els mateixos per a qualsevol altra cara.

Per a n gran, la distribució binomial i la distribució gaussiana donen valors semblants. Per tant, la funció de probabilitat del valor O_k és pot suposar que és gaussiana, de manera que la funció densitat de probabilitat per a

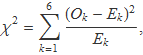
és la khi quadrat per a 5 graus de llibertat. En lloc d'haver de calcular l'histograma de la Fig. 2 fent simulacions, es pot suposar que l'histograma sortirà amb la forma de la funció densitat de probabilitat de χ². La semblança amb l'histograma de la Fig. 2 s'il·lustra a la Fig. 4.

Es tenen 5 graus de llibertat perquè

de manera que els valors O₁, O₂, O₃, O₄ i O₅ determinen el de O₆.

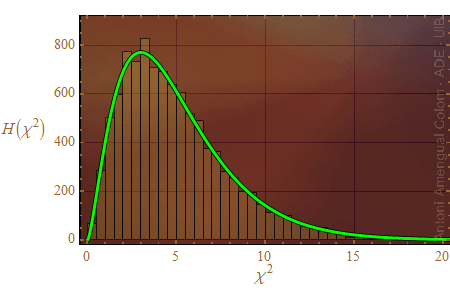
Figura 4. Histograma de la Fig. 2 comparat amb la funció densitat de probabilitat khi quadrat per a 5 graus de llibertat multiplicada pel nombre de sèries incloses a l'histograma (deu mil).

Per determinar la probabilitat que un dau legal doni una sèrie amb χ² més gran que un valor donat, per exemple, 8.52 (que és el que dóna la sèrie de l'histograma esquerra de la Fig. 1), es pot usar directament la funció densitat de probabilitat de khi quadrat.

La integral de la funció densitat de probabilitat khi quadrat des de χ₀² = 8.52 fins a infinit,

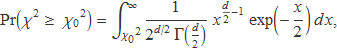
és la probabilitat que un dau sense trucar generi una sèrie amb un valor de khi quadrat tan o més gran que l'obtingut. La integració dóna

Pr(χ² ≥ 8.52) = 12.98%.

Una probabilitat que és consistent amb el valor ja calculat a partir de la simulació de 10000 sèries.

Més que calcular la integral, es pot consultar el valor en una taula o sobre el gràfic per a g = 5. En el gràfic s'ha de mirar la probabilitat corresponent a 8.52/g = 1.70.

Es vol analitzar si un dau és legal usant una sèrie de 600 llançaments. Les passes a donar són les següents:

1) Es realitza una sèrie de 600 llançaments i és compte el nombre de vegades O_k que surt cada cara. Els valors es poden recollir en un histograma.

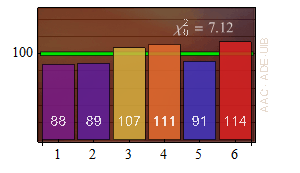
Mostra resultats dels 600 llançaments »

2) Es calcula

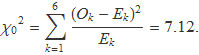
3) Es determina la probabilitat

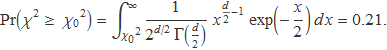
Més que calcular la integral, es pot consultar el valor en una taula o sobre el gràfic per a g = 5. En el gràfic s'ha de mirar la probabilitat corresponent a 7.21/g = 1.44. Per a 1.4 es té 22.1% i, per a 1.5, 18.6%. La interpolació lineal dóna 21%.

4) Conclusió:

La probabilitat 0.21 obtinguda significa que 21 de cada 100 sèries de 600 llançaments donaran un valor de khi quadrat igual o superior a 7.12. Aquesta probabilitat és superior al 5%. Per tant, la discrepància entre l'histograma obtingut i el teòric no és significativa. El dau es considera legal.