
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Presentació de resultats
Xifres significatives
Introducció «
El nombre de xifres que s'han d'escriure per presentar un resultat experimental o un valor calculat està determinat per la incertesa: Les centèsimes són irrellevants si no s'està segur de la validesa de les dècimes; es poden usar si s'han de calcular altres variables, però no té sentit escriure-les en el resultat final.
En aquest tema es presenta primer la definició de xifra significativa i es dóna un criteri per expressar la incertesa. Això és necessari perquè la incertesa del valor d'una variable determina el nombre de xifres significatives amb que s'ha d'expressar el valor.
Quines són les xifres significatives d'un número?
 «
«
Les xifres significatives d'un número són:
• Les xifres 1, 2, 3, 4, 5, 6, 7, 8 i 9.
• Les xifres 0 entre xifres de l'1 al 9 (hi pot haver el punt decimal enmig, per exemple, el 0 de 1.02 és una xifra significativa).
• Les xifres 0 en les xifres a la dreta del punt decimal en números més grans que 1 (per exemple, el zero de 1.0 és una xifra significativa).
Els números de la primera columna de la Taula 1 tenen una xifra significativa; els de la segona columna, dues; i els de la tercera, tres.
| 1 | 2 | 3 |
| 0.002 | 0.027 | 0.0274 |
| 0.2 | 1.0 | 1.02 |
| 2 | 2.7 | 2.74 |
| 20 | 27 | 27.4 |
| 200 | 270 | 274 |
Taula 1. Exemples de números amb n = 1, 2 o 3 xifres significatives.
Atenció amb els nombres sencers «
Els zeros en un número sencer poden ser significatius o no. Si un comptatge de partícules dóna 200 exactament, el número tendrà tres xifres significatives; però si ha donat 197 i es presenta com a resultat «200 aproximadament», el número només tendrà una xifra significativa. Escriure «exactament» o «aproximadament» pot donar informació sobre el nombre de xifres significatives del número sencer. Una alternativa és escriure el número sencer com a un número real amb notació exponencial. Així, el número 2.00×102 té clarament tres xifres significatives i 2.0×102 només dues.
Amb quantes xifres significatives s'ha d'escriure un número?
 «
«
El nombre de xifres significatives d'un valor està limitat per la incertesa.
Com s'ha indicat a la introducció, per a un rectangle de costats 20.4 cm i 12.7 cm, el teorema de Pitàgores dóna la longitud de la diagonal
![]()
però no totes le xifres són significatives perquè si els costats fossin lleugerament més llargs, 20.41 cm i 12.71 cm per exemple, es calcularia
![]()
Els dos resultats són diferents a partir del segon decimal. És necessari saber amb quina exactitud es coneixen les longituds dels costats per saber si la centèsima és una xifra significativa de la longitud de la diagonal.
Per determinar el nombre de xifres significatives d'un número, primer s'ha de saber determinar les xifres significatives de la incertesa.
Xifres significatives de la incertesa
 «
«
El número que representa la incertesa amb que es coneix una quantitat es donarà amb una xifra significativa, o amb dues quan formin una de les parelles
10, 11, 12, 13, 14, 15, 16, 17, 18 o 25.
Aquesta no és una norma general, però està basada en que l'arrodoniment de la incertesa no augmenti massa. L'arrodoniment a 1 o a 2 d'una incertesa igual a 1.4 cm disminueix o augmenta la incertesa excessivament. La diferència entre 2 i 1.4 és quasi bé el 43 per cent d'1.4.
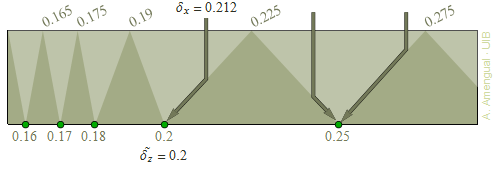
Figura 2. Il·lustració de l'arrodoniment de la incertesa en forma de serralada. En els vèrtex inferiors de cada vall hi ha els valors acceptables. La vall a la que caurà un valor correspon al valor de la incertesa amb el nombre de xifres adient.
Com s'ha d'arrodonir a dues xifres significatives el número 0.225 que està sobre una punta de la serralada de la Fig. 2? Quedarà arrodonit a 0.2 o a 0.25? La resposta és que la incertesa s'ha d'expressar amb alguns decimals més. Si el número és 0.225001, s'ha d'arrodonir a 0.2; però si és 0.224998, s'ha d'arrodonir a 0.25. En cas que sigui exactament 0.225, es pot presentar com a 9/40.
En general, la incertesa s'ha de calcular amb tres xifres significatives (o més si la que queda a la dreta és zero), i presentar-la amb una xifra o dues si es considera pertinent. A la taula següent es mostren incerteses calculades amb tres xifres arrodonides segons s'ha indicat.
| 960 ≈ 1000 | 182 ≈ 180 | 265 ≈ 250 |
| 107 ≈ 110 | 187 ≈ 180 | 275 ≈ 300 |
| 122 ≈ 120 | 192 ≈ 200 | 287 ≈ 300 |
| 132 ≈ 130 | 205 ≈ 200 | 318 ≈ 300 |
| 143 ≈ 140 | 214 ≈ 200 | 347 ≈ 300 |
| 148 ≈ 150 | 232 ≈ 250 | 381 ≈ 400 |
| 158 ≈ 160 | 246 ≈ 250 | 402 ≈ 400 |
| 171 ≈ 170 | 252 ≈ 250 | 451 ≈ 500 |
Taula 2. Exemples d'incerteses arrodonides. S'han remarcat dos casos per recordar que 0.19 no es posa amb el criteri usat aquí.
A la taula següent es presenten números amb les mateixes xifres significatives, però expressats amb una unitat més gran que en la taula anterior, de manera que, per exemple, 960 ara és 0.096.
| 0.096 ≈ 0.1 | 18.2 ≈ 18 | 26.5 ≈ 25 |
| 0.107 ≈ 0.11 | 1.87 ≈ 1.8 | 2.75 ≈ 3 |
| 1.22 ≈ 1.2 | 1.92 ≈ 2 | 28.7 ≈ 30 |
| 13.2 ≈ 13 | 20.5 ≈ 20 | 0.318 ≈ 0.3 |
| 1.43 ≈ 1.4 | 2.14 ≈ 2 | 3.47 ≈ 3 |
| 14.8 ≈ 15 | 23.2 ≈ 25 | 38.1 ≈ 40 |
| 15.8 ≈ 16 | 2.46 ≈ 2.5 | 40.2 ≈ 40 |
| 17.1 ≈ 17 | 2.52 ≈ 2.5 | 0.451 ≈ 0.5 |
Taula 3. Exemples d'incerteses arrodonides.
Es poden donar resultats amb dues xifres qualsevol si el resultat s'ha obtingut amb una mesura feta amb molta atenció (vegeu l'apartat posterior «Llegint constants físiques a Viquipèdia»). No obstant això, aquí aplicarem el criteri descrit.
La resposta a «amb quantes xifres significatives s'ha d'escriure un número?»
 «
«
El nombre de xifres significatives que s'han d'escriure en donar un resultat depèn de la incertesa. Suposem que el resultat d'unes operacions dóna x = 8.314472. A continuació hi ha tres exemples amb incerteses δx diferents:
• Si δx = 0.123, s'arrodoneix δx = 0.12. Les xifres significatives de x seran el 8 i els dos primers decimals (3 i 1). D'aquesta manera, suposant unes unitats per a x com les que té la constant dels gasos, s'ha de presentar x = 8.31 ± 0.12 J K–1 mol–1.
• Si δx = 0.204, s'arrodoneix δx = 0.2. Les xifres significatives de x seran el 8 i el primer decimal. D'aquesta manera, s'ha de presentar x = 8.3 ± 0.2 J K–1 mol–1.
• Si δx = 0.257, s'arrodoneix δx = 0.25. Les xifres significatives de x seran el 8 i els dos primers decimals arrodonits a un múltiple de 0.25. D'aquesta manera, s'ha de presentar x = 8.25 ± 0.25 J K–1 mol–1.
El significat del símbol ± s'aprèn normalment amb l'expressió que dóna les dues solucions d'una equació de segon gran. El significat aquí és lleugerament diferent, x = 5 ± 2 indica que el valor de la variable x està entre 3 i 7.
Si les primeres xifres significatives són iguals a 96, 97, 98 o 99 i la incertesa és inferior a la unitat, com 0.097 i 0.97, convé arrodonir afegint un 0 a la dreta. Així, les incerteses 0.097 i 0.97 convé expressar-les 0.10 i 1.0. D'aquesta manera, un resultat de 8.642 amb la incertesa 0.097 s'expressarà 8.64 ± 0.10. Si la incertesa és superior a la unitat, el zero apareix directament amb l'arrodoniment, 86.4 ± 9.7 dóna 86 ± 10.
Quan el número considerat és molt gran o molt petit, convé expressar-lo usant potències de 10. No hi ha un criteri establert, però a la taula adjunta se'n suggereix un. La incertesa s'escriu amb un màxim de 3 o 4 xifres comptant els zeros.
| n | δx = 0.124 10n | δx = 0.201 10n | δx = 0.257 10n |
| -7 | (36342 ± 12) × 10-9 | (3634 ± 2) × 10-8 | (36350 ± 25) × 10-9 |
| -6 | (36342 ± 12) × 10-8 | (3634 ± 2) × 10-7 | (36350 ± 25) × 10-8 |
| -5 | (36342 ± 12) × 10-7 | (3634 ± 2) × 10-6 | (36350 ± 25) × 10-7 |
| -4 | 0.036342 ± 0.000012 | 0.03634 ± 0.00002 | 0.036350 ± 0.000025 |
| -3 | 0.36342 ± 0.00012 | 0.3634 ± 0.0002 | 0.36350 ± 0.00025 |
| -2 | 3.6342 ± 0.0012 | 3.634 ± 0.002 | 3.6350 ± 0.0025 |
| -1 | 36.342 ± 0.012 | 36.34 ± 0.02 | 36.350 ± 0.025 |
| 0 | 363.42 ± 0.12 | 363.4 ± 0.2 | 363.50 ± 0.25 |
| 1 | 3634.2 ± 1.2 | 3634 ± 2 | 3635.0 ± 2.5 |
| 2 | 36342 ± 12 | 36340 ± 20 | 36350 ± 25 |
| 3 | 363420 ± 120 | (3634 ± 2) × 102 | 363500 ± 250 |
| 4 | (36342 ± 12) × 102 | (3634 ± 2) × 103 | (36350 ± 25) × 102 |
| 5 | (36342 ± 12) × 103 | (3634 ± 2) × 104 | (36350 ± 25) × 103 |
| 6 | (36342 ± 12) × 104 | (3634 ± 2) × 105 | (36350 ± 25) × 104 |
| 7 | (36342 ± 12) × 105 | (3634 ± 2) × 106 | (36350 ± 25) × 105 |
Taula 4. Exemples de l'expressió de diversos valors amb incerteses diferents.
Llegint constants físiques a Vikipèdia
 «
«

La constant de Planck s'ha mesurat amb precisió i val
h = (6.62606957 ± 0.00000029) × 10–34 J s.
El valor i la incertesa es podrien donar d'altres maneres, per exemple, posant la constant i la incertesa amb que es coneix sense decimals,
h = (662606957 ± 29) × 10–42 J s.
Una altra manera és escriure les xifres de la incertesa entre parèntesis just després del valor,
h = 6.62606957 (29) × 10–34 J s.
Aquesta és la notació que s'usa en moltes de les taules de Vikipèdia. Es pot mirar, per exemple, la pàgina amb les taules de constants físiques.
Aquests són tres exemples amb les dues notacions:
5.432(1) = 5.432 ± 0.001,
78.76(12) = 78.76 ± 0.12,
9.678(42) = 9.678 ± 0.042.
