
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Distribució normal (gaussiana)
La distribució de Student i l'error estàndard de la mitjana
Introducció «
Per començar la lectura d'aquest tema s'ha de recordar que l'error estàndard de la mitjana ee de n valors {x1, x2, ..., xn} d'una variable aleatòria x amb funció de distribució de probabilitat gaussiana, és igual a la desviació estàndard sn de la mostra dividida per l'arrel de n,
![]()
Quan n augmenta, la funció de probabilitat de les mitjanes de grups de n valors {x1, x2, ..., xn} tendeix a una gaussiana centrada en el valor mitjà de les mitjanes i amb una desviació estàndard igual a l'error estàndard ee.
Una variable s'ha mesurat quatre vegades amb presència d'errors aleatoris i s'ha obtengut 223, 210, 214 i 208 amb unes unitats que no són rellevants per haver d'indicar-les aquí. La mitjana d'aquest grup de quatre valors i l'error estàndard donen l'estimació 214 ± 3. A la Taula 1 es recull aquest resultat i els resultats d'altres mesures fetes en les mateixes condicions.
Com s'obté 214 ± 3? »
| # | x | m ± s4 |
| 1 | 223, 210, 214, 208 | 214 ± 3 |
| 2 | 224, 239, 218, 241 | 230 ± 6 |
| 3 | 229, 222, 211, 207 | 217 ± 5 |
| 4 | 230, 219, 210, 214 | 218 ± 4 |
| 5 | 217, 203, 235, 242 | 224 ± 9 |
Taula 1. Cinc grups de 4 mesures d'una variable amb presència d'errors aleatoris, amb la mitjana i l'error estàndard de cada grup presentat a la darrera columna.
L'error estàndard dels grups de la Taula 1 fluctua bastant. S'intueix que la distància entre la mitjana d'un grup i la mitjana real pot ser superior a dues vegades l'error estàndard amb probabilitat gran (les barres d'error s'han dibuixat a la Fig. 1). La possibilitat d'aquesta discrepància genera un problema dins un laboratori quan s'ha de calcular una mitjana a partir de poques mesures. Ni la mitjana ni l'error estàndard seran fiables.
A vegades no es poden fer més mesures i només es té la mitjana calculada amb les poques mesures disponibles. En tal cas, se sap que la incertesa serà més gran que l'error estàndard calculat. L'interval dins el qual s'ha d'esperar trobar la mitjana poblacional amb probabilitat alta és més ampla que l'interval determinat per l'error.
L'ampliació de l'interval al voltant de la mitjana es fa multiplicant l'error estàndard pel factor de Student que depèn del nombre de dades amb les que s'ha calculat la mitjana. A la Taula 2 es donen els valors d'aquest factor per a diferents nombres de dades i els dos intervals de confiança que se solen usar, el 95 % i el 99 %.
Quan es necessitin els valors, es pot obrir aquest tema o accedir a la taula des de l'apartat de taules de l'índex.
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 20 | 50 | 100 |
| t95% | 4.30 | 3.18 | 2.78 | 2.57 | 2.45 | 2.36 | 2.31 | 2.26 | 2.23 | 2.20 | 2.18 | 2.16 | 2.14 | 2.09 | 2.01 | 1.98 |
| t99% | 9.92 | 5.84 | 4.60 | 4.03 | 3.71 | 3.50 | 3.36 | 3.25 | 3.17 | 3.11 | 3.05 | 3.01 | 2.98 | 2.86 | 2.68 | 2.63 |
Taula 2. Valors per corregir l'error estàndard quan s'ha calculat amb poques dades.
Per a un conjunt de n valors, s'espera que la mitjana poblacional μ estigui dins l'interval
![]()
o, escrit en forma de valor i incertesa,
![]()
Com es pot suposar, el factor t tendeix a 1 quan n creix, però cal observar a la Taula 2 que l'error estàndard calculat a partir de entre 50 i 100 mesures encara s'ha de duplicar per tenir la mitjana poblacional dins l'interval d'incertesa amb una probabilitat del 90%.
La Fig. 1 il·lustra que la discrepància entre alguns valors de la Taula 1 és significativa, però deixa de ser-ho quan la incertesa s'augmenta amb el factor de Student.
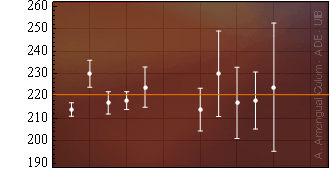
Figura 1. Les cinc barres de l'esquerra mostren els valors de la Taula 1. Les cinc barres de la dreta mostren els mateixos valors amb la barra d'error multiplicada per t95%(4). La línia horitzontal taronja correspon a la mitjana dels cinc valors.
Els valors de la taula  «
«
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| t95% | 4.30 | 3.18 | 2.78 | 2.57 | 2.45 | 2.36 | 2.31 | 2.26 |
| t99% | 9.92 | 5.84 | 4.60 | 4.03 | 3.71 | 3.50 | 3.36 | 3.25 |
Figura 5. Gràfics de la densitat de probabilitat t de Student per a diferents valors de n. L'àrea verda és el 95% de l'àrea total. Les fletxes marquen els límits del domini que dóna aquesta àrea i del domini que dóna el 99% de l'àrea.
Els valors que figuren a la Taula 2 són els valors de tp(n) per a p = 95% i 99% que satisfan l'equació
![]()
A la Fig. 5 s'il·lustra el significat d'aquests valors per a n entre 3 i 10. La part de la Taula 2 per a aquests valors de n es mostra a baix de la figura.
Il·lustració de l'efecte del factor de Student  «
«
A la Fig. 1 ja s'ha il·lustrat l'efecte del factor de Student ampliant la barra d'error. Allà s'han usat els errors estàndards de cinc grups de quatre mesures, multiplicats pel factor t90(4), per dibuixar la barra d'error a cada costat de les mitjanes. A la Fig. 6, es dibuixen gaussianes centrades en les mitjanes de cada grup de quatre mesures. Les desviacions estàndards són els errors estàndards de cada grup. L'abscissa del segment vertical de color blanc és la mitjana de les cinc mitjanes. L'abscissa de la línia vertical de color taronja és la mitjana incloent un nombre gran de mesures i, per tant, s'acosta bastant a la mitjana de la població.
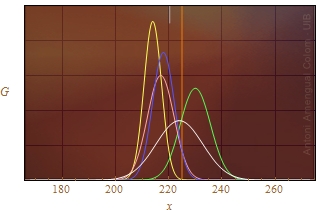
Figura 6. Funcions gaussianes de mitjanes μ = m i σ = sn dels cinc grup de mesures de la Taula 1. Quan es posa el cursor sobre la figura, la desviació estàndard es multiplica per un factor de Student (l'escala de les ordenades no s'ha marcat perquè no és rellevant aquí i tanmateix seria diferent en les dues imatges).
La línia taronja de la Fig. 6 cau a la dreta del domini on la coa de la gaussiana de color groc es veu per damunt de l'eix. Aquesta gaussiana correspon a un grup de mesures que ha donat circumstancialment l'error estàndar més petit. Si només es tingués aquesta mitjana amb l'error estàndard i s'oblidés que s'ha obtengut amb només quatre mesures, semblaria que es té un resultat amb una incertesa baixa. El problema seria que la probabilitat que la mitjana de la població fos igual a l'abscissa de la línia taronja és consideraria pràcticament nul·la. Aquesta mesura i l'anàlisi estadístic limitat conduiria a un resultat incorrecte. Arribats a aquetes línies, ja se sap que el problema sorgeix perquè la desviació estàndard és incerta quan es calcula a partir de poques mesures. En el requadre a part es recull com ho digué Gosset àlies Student..
«El mètode usual de determinar la probabilitat que la mitjana de la població es trobi dins una distància donada de la mitjana de la mostra és assumir que la distribució al voltant de la mitjana de la mostra es normal amb una desviació estàndar igual a s/ , on s és la desviació estàndard de la mostra, i utilitzar llavors les taules de la integral de probabilitat.»
, on s és la desviació estàndard de la mostra, i utilitzar llavors les taules de la integral de probabilitat.»
»Però, a mesura que es disminueix el nombre d'experiments, el valor de la desviació estàndard trobat a partir de la mostra d'experiments esdevé ell mateix subjecte a un error creixent, fins que els judicis assolits d'aquesta manera es poden convertir en totalment enganyosos.»
Les gaussianes de la Fig. 6 modificades augmentant l'amplada amb el factor de Student es poden veure posant el cursor sobre la Fig. 6. La nova línia groga indica que la mesura i la nova incertesa inclouen el valor de la mitjana de la població amb una probabilitat, ara sí, notable.

