
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Propagació de l'error
Càlcul de l'error de la funció inversa:
El coeficient de restitució
Introducció «
La determinació de la incertesa d'una variable u calculada a partir d'una altra variable w, quan es disposa de la funció w(u) i no resulta fàcil obtenir la funció inversa u(w), s'ha de fer amb un dels dos procediments descrits en aquest tema. L'exemple analitzat és la determinació del coeficient de restitució d'una pilota quan bota sobre un sòl rígid a partir dels temps entre rebots.
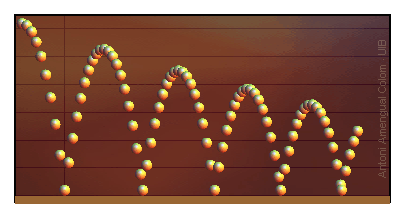
Figura 1. Simulació de l'altura en funció del temps en unitats arbitràries d'una pilota que rebota sobre una superfície.
La fracció de l'energia mecànica de la pilota perduda en un rebot depèn del tipus de pilota, la velocitat abans de l'impacte i les característiques de la superfície. Aquí només es consideraran velocitats baixes que permetran negliglir la fricció amb l'aire i suposar que la fracció perduda de l'energia mecànica no depèn de la velocitat, de manera que hi ha una constant de proporcionalitat e, l'anomenat coeficient de restitució de la pilota sobre la superfície, que dóna la velocitat després del rebot a partir de la velocitat prèvia,
vdesprés = e vabans.
La lletra e no s'usarà aquí per a l'espai recorregut com és habitual en les fórmules de cinemàtica, e és el coeficient de restitució.
Els instants quan la pilota rebota
 «
«
Una pilota pot arribar perpendicularment a una superfície rugosa i rebotar cap a un costat. Sobre un superfície plana, la pilota també pot rebotar cap a un costat per la manera com es comprimeix durant la col·lisió i recupera la forma després. En l'anàlisi que es fa aquí, se suposa que la component horitzontal de la velocitat és zero o es manté constant i el seu valor no importa.
Una pilota es deixa caure sobre una superfície rígida i plana. Sigui v0 la velocitat vertical de la pilota abans de la col·lisió. La pilota rebota i parteix per amunt amb la velocitat
v1 = e v0.
Negligint el fregament amb l'aire, la pilota pujarà, caurà i tornarà xocar amb la superfície amb velocitat v1. La velocitat amb que sortirà rebotada la pilota serà
v2 = e v1 = e2 v0.
La velocitat de la pilota just després de n rebots serà
vn = e vn–1 = e2 vn–2 = ... = en v0.
El temps entre un rebot i el següent es pot calcular cercant el temps que ha de passar perquè la velocitat de la pilota canviï de signe per l'acceleració de la gravetat,
– vn = vn – g t.
Aïllant el temps, es troba que l'interval τn entre els rebots n i n + 1 és
![]()
En funció de v0,
![]()
Si el cronòmetre es posa a zero quan la pilota rebota per primera vegada, el temps tn quan la pilota fa el rebot número n (n > 1) és
tn = τ1 + τ2 + ... + τn−1.
Notant que
![]()
es pot escriure
![]()
En aquest càlcul, s'ha negligit la durada de la col·lisió, el temps durant el qual es produeix precisament la pèrdua d'energia cinètica de la pilota.
Càlcul del coeficient de restitució i la incertesa a partir dels temps entre rebots
 «
«
Mesurant l'interval τ1 entre els rebots primer i segon, i el temps tn entre el primer i l'enèsim, es té una equació polinòmica per calcular el coeficient de restitució
1 + e + e2 + ... + en–2 = Tn
amb n > 1 i
![]()
El valor de Tn és el quocient entre dos temps i no tendrà unitats, com tampoc les té el coeficient de restitució.
Procediment directe per a 3 rebots
 «
«
Si es cronometren tres rebots, el temps entre el primer i el segon és τ1 i entre el primer i el tercer, t3. Llavors,
1 + e = T3.
La incertesa del valor del coeficient de restitució és igual a la incertesa de T3, la qual depèn de les incerteses de les mesures de t3 i τ1.
Procediment directe per a 4 rebots
 «
«
Si es cronometren quatre rebots, el temps entre el primer rebot i el quart és t3 i el coeficient de restitució és la solució de l'equació de segon grau
1 + e + e2 = T4.
La solució positiva és
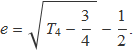
La incertesa sobre el valor del coeficient de restitució es pot calcular encara fàcilment en aquest cas. Considerant e com una funció de T4 es calcula
![]()
La darrera igualtat s'ha emmarcat per comparar amb un càlcul que es farà a continuació.
Procediment general per a 3 o més rebots
 «
«
El coeficient de restitució s'ha de calcular resolent l'equació polinòmica
1 + e + e2 + ... + en–2 = Tn,
de grau superior a dos. La funció e(Tn) no es podrà escriure de manera senzilla i no es podrà fer la derivada del coeficient e respecte de Tn. Ara bé, es pot usar la relació entre derivades
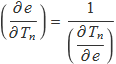
per calcular
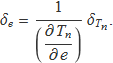
Feta la derivada s'obté la incertesa del valor del coeficient de restitució
![]()
L'aplicació al cas n = 3, dóna directament la igualtat entre les incerteses de e i Tn.
L'aplicació al cas n = 4, dóna el mateix resultat requadrat a l'apartat anterior:
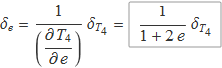
L'expressió obtinguda mostra que la incertesa disminueix quan el nombre de rebots cronometrats augmenta.
Un altre càlcul de la incertesa sobre el coeficient de restitució
 «
«
Amb les solucions de les equacions
![]()
![]()
es tendran els valors màxim i mínim que cal esperar pel coeficient de restitució degut a la incertesa de Tn.
La línia verda de la Fig. 1 correspon a Tn – δTn i la línia vermella, a Tn + δTn. La línia groga és la funció 1 + e + ...+ en. La zona de fons més clar marca el domini de l'eix d'abscisses dins on està el valor del coeficient de restitució. Dins la figura s'ha inclòs una imatge per representar les posicions d'una pilota a determinats intervals de temps i mostrar el nombre de rebots del cas considerat.
L'amplada de la zona de fons clar disminueix quan es cronometren més rebots, indicant que la incertesa sobre el valor del coeficient de correlació calculat amb Tn més gran disminueix.
Figura 2. Les interseccions de la corba groga amb línies verda i vermella determinen l'interval d'incertesa del valor del coeficient de restitució.
