
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Propagació dels errors aleatoris
Quocient de dues variables aleatòries gaussianes
Introducció «
La funció densitat de probabilitat d'una variable u que és el quocient de dues variables aleatòries gaussianes es pot calcular analíticament i es presenta en aquest tema com exemple per comparar la funció exacta amb la funció obtinguda amb el càlcul aproximat descrit en els temes anteriors.
Es mostra que la funció densitat de probabilitat del quocient és pràcticament gaussiana amb una variància que es pot calcular a partir de les variàncies de les variables que intervenen en el quocient si les variàncies són petites. La importància d'aquesta aproximació és justificar el càlcul de la propagació de l'error al dividir variables físiques amb una barra d'error petita.
Càlcul exacte «
Siguin X1 i X2 dues variables aleatòries gaussianes amb funcions densitat de probabilitat
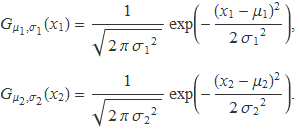
Se cercarà aquí la funció densitat de probabilitat de la variable
![]()
Un valor u = u0 es pot obtenir d'infinites maneres. Per a tot valor de x1, el valor x2 = x1 / u0 dóna u0 quan es divideixen. Per tant, la funció densitat de probabilitat sense normalitzar per a u = u0 és
![]()
Usant l'expressió de les gaussianes, s'escriurà
![]()
Les arrels quadrades són constants i poden sortir fora de la integral, i els exponents es poden sumar. Deixant les constants de banda es posarà a continuació el signe de proporcionalitat en lloc del signe d'igualtat:
![]()
Usant taules d'integració es troba que
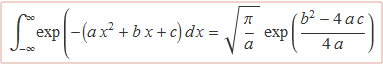
La integral que dóna S(u0) es pot escriure d'aquesta manera. Desenvolupant els termes i identificant el terme independent i els coeficients que multipliquen a x i a x2, es troba
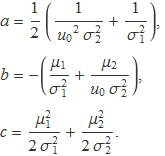
Després de bastants operacions es troba que
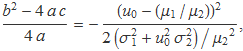
de manera que
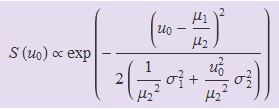
Càlcul aproximat
 «
«
La variable u és
![]()
Les derivades parcials de la funció són
![]()
![]()
El valor d'aquestes derivades per a x1 = μ1 i x2 = μ2 s'usen per escriure el desenvolupament en sèrie de Taylor de la funció u fins a primer ordre,
![]()
La funció queda aproximada com és habitual per una combinació lineal de les dues variables:
![]()
La variància de la suma de variables aleatories gaussianes és
![]()
El terme u0 = μ1 / μ2 és constant i no contribueix a la variància de la variable u. En conseqüència, l'aproximació per a la variància de la funció densitat de probabilitat Saprox(u) és
![]()
Usant aquesta variància per escriure el resultat en forma de gaussiana, es troba
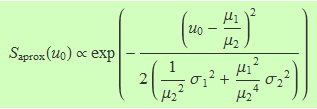
Comparació dels dos càlculs
 «
«
Sense incloure el factor de normalització, les funcions densitat de probabilitat exacta i aproximada es tornen escriure a continuació amb els termes diferents dins un rectangle groc
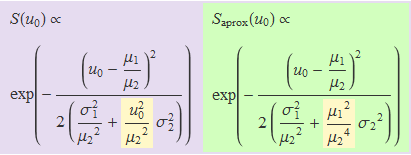
En el càlcul de l'expressió exacte, u0 apareix en el denominador, però en el càlcul aproximat, no. Les exponencials de les dues expressions donen el mateix valor per a u0 = μ1 / μ2 i difereixen per a altres valors de u0. Però la diferència és poca si els termes de primer ordre de l'aproximació de Taylor són petits,
![]()
Per donar un exemple concret, s'han considerat els valors
x1 = 20 ± 0.5,
x2 = 10 ± 0.5.
Per aquests valors es troba
![]()
La línia vermella de la Fig. 1 correspon a l'exponencial de S(u0) i la línia verda a l'exponencial de l'aproximació.
La imatge mostra que usar l'arrel de 0.112 com la desviació estàndard per donar el resultat
u = 2.00 ± 0.33
és una bona aproximació i millorarà si les incerteses sobre x1 i x2 són més petites.
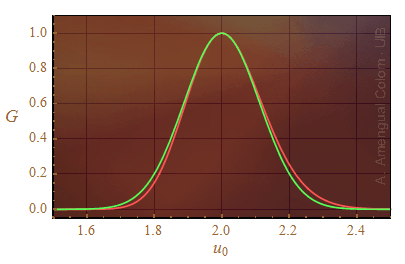
Figura 1. Comparació de les funcions densitat de probabilitat aproximada (línia verda) i exacta del quocient entre dues variables aleatòries gaussianes.
