
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Distribució de Poisson
Norma, valor esperat i variància
Introducció «
La funció de probabilitat de Poisson és
![]()
En aquest tema, es mostrarà la forma de la funció per a diversos valors de μ i després es demostrarà que la suma per a k des de zero fins a infinit val 1. Posteriorment, es calcularan el valor esperat E(k) i la variància σ2. Es trobarà que el valor esperat i la variància són ambdues iguals a μ,
![]()
En les demostracions presentades a continuació, s'usa el desenvolupament de la funció exponencial en sèrie de Taylor.
Representació gràfica «
Figura 1. Els punts verds representen els valors de la funció de probabilitat de Poisson Pμ. la línia groga és la gaussiana de mitjana μ i variància μ2 i es dibuixa per a comparar-les.
Normalització «
Es demostrarà que la funció de probabilitat de Poisson està normalitzada, de manera que
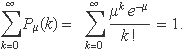
La demostració és quasi directa. El terme e–μ no depèn de k i es pot treure factor comú,
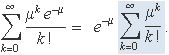
El sumatori destacat en color és el desenvolupament en sèrie de Taylor de la funció exponencial avaluada en el punt μ, així que directament resulta
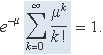
Valor esperat (primer càlcul) «
El valor esperat de k és, per definició,
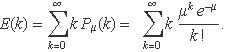
Per fer la suma s'usarà que el primer terme k = 0 no contribueix a la suma, que k! = k (k – 1)! per a k ≥ 1, i que la constant e–μ es pot treure del sumatori. S'escriurà
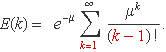
El canvi de l'índex de suma k per
m = k – 1
dóna
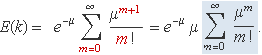
El sumatori destacat en color torna ser eμ (aquest pic l'índex mut és m) que es cancel·la amb l'exponencial que prové de la normalització i s'obté
![]()
Valor esperat (segon càlcul)
 «
«
Es parteix de la normalització de la funció de probabilitat de Poisson
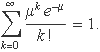
Com que el sumatori és una constant (la unitat), la derivada és zero:
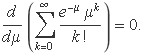
La derivada d'un sumatori és la suma de derivades,
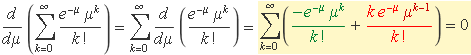
El sumatori del terme de color verd val –1 perquè és el mateix que el de partida canviat de signe. El terme de color vermell, després d'extreure μ-1 fora del sumatori, dóna la definició del valor esperat de k. Per tant,
![]()
Aïllant, el valor esperat s'obté de nou
![]()
Variància
 «
«
El càlcul de la variància es presenta separat en tres passes.
Pas 1 «
La variància de la distribució de Poisson és, per definició,

Desenvolupant el quadrat es té
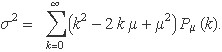
Separant en tres sumatoris, queda
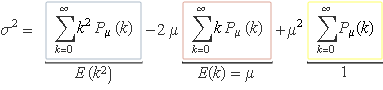
Els resultats dels sumatoris requadrats s'han indicat a l'expressió anterior. El primer sumatori és la definició del valor esperat de k2, el segon val μ perquè és el valor esperat de k, i el tercer val 1 perquè és la condició de normalització. Fetes les multiplicacions per les constants fora dels requadres, els termes segon i tercer donen –μ2 de manera que la variància serà coneguda si es coneix E(k2):
![]()
Pas 2. Càlcul del valor esperat de k2 «
Per avaluar el valor esperat de k2 es derivarà la igualtat de la normalització
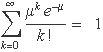
dues vegades respecte de μ. La primera derivada s'ha fet abans en el segon càlcul del valor esperat de k. El resultat de derivar la igualtat una vegada era
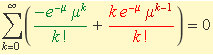
Aquesta igualtat es torna derivar respecte de μ i s'obté

Els sumands s'escriuran per separat. El terme destacat (k – 1) k = k2 – k també se separarà en dos sumands. Així s'escriu
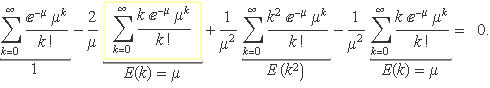
El resultat de cada sumatori s'ha indicat a l'expressió anterior, la qual dóna
![]()
Aïllant el valor esperat de k2 s'obté
![]()
Pas 3 «
Substituint el valor esperat de k2 dins l'expressió de la variància obtinguda al final del primer pas es troba
![]()
Aisí s'obté finalment la variància de la funció de probabilitat de Poisson,
![]()
