
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Propagació de l'error
Derivades parcials
Introducció «
L'energia cinètica d'un mòbil depèn de la seva massa i la velocitat amb la que es mou. L'energia potencial gravitatòria d'un objecte depèn de la seva massa, l'acceleració de la gravetat i la distància a un nivell de referència. El període d'oscil·lació d'una esfera penjada d'una molla, depèn de la massa de l'esfera i la constant elàstica de la molla. La variació de temperatura d'una peça de metall depèn de la seva capacitat calorífica i la quantitat de calor que intercanvia amb el medi on es troba. Moltes equacions físiques s'enuncien i escriuen aïllant una magnitud en funció d'altres. En els casos esmentats:
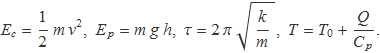
De manera general, s'aïlla una magnitud física per expressar-la en funció d'altres que s'anomenaran variables. Si la magnitud es diu u i les variables es diuen x, y, z..., matemàticament s'escriu
![]()
Es poden usar diverses notacions per indicar la derivada de la funció u respecte de x mantenint les altres variables constants. S'usen àmpliament les tres notacions equivalents:
![]()
Qui sàpiga derivar funcions d'una variable no ha de tenir cap problema per fer derivades parcials. Les variables respecte de les quals no es deriva es tracten com les constants. Per exemple, amb
![]()
es té
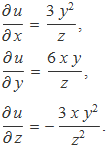
Per què interessen les derivades parcials en l'anàlisi de dades?
 «
«
Les derivades parcials interessen perquè permeten quantificar la variació d'una funció degut a la variació del valors de les variables. Les derivades parcials s'usen per propagar l'error i fixar la incertesa sobre un valor calculat a partir d'altres.
Addicionalment, una funció es pot aproximar per un polinomi (sèries de Taylor) els coeficients del qual s'obtenen amb derivades parcials de la funció considerada.
