Conèixer la incertesa dels valors amb els quals s'està fent un càlcul és necessari per prendre decisions segons els resultats. La determinació de la incertesa és, per tant, una tasca ineludible quan es fan mesures o càlculs numèrics.

Fer una mesura sense determinar l'error experimental del resultat no és útil.

La incertesa sobre un valor també s'anomena error. Aquesta altra paraula té una connotació negativa quan és sinònim d'equivocació però no la té dins el context de les mesures experimentals i els càlculs numèrics. Quan es dóna l'error sobre un valor, s'està acotant la diferència entre el valor obtingut i el valor real desconegut.

Es presenten a continuació alguns motius per fer mesures precises amb exemples. En el tema següent es comentaran tres casos que remarquen la importància de conèixer la incertesa sobre el valor obtingut en una mesura.

Pitja el botó «Només Títols» del menú per veure els títols dels apartats sense el contingut. Després, pitja sobre un dels símbols » per veure el contingut de l'apartat, o el botó «Veure Tot» del menú per obrir tots els apartats.

La Fig. 1 il·lustra i explica el mètode d'Eratòstenes per calcular el radi de la Terra a partir de la distància entre Alexandria i Syene, i de la mida d'una ombra d'un pal vertical a Alexandria el migdia del solstici d'estiu. La llum directa del Sol arribava al fons dels pous de Syene, actualment Assuan, però no a Alexandria. Aquest fet es podia entendre amb una terra esfèrica, el radi de la qual es podia calcular amb trigonometria.

La seperació entre les dues ciutats egípcies es mesurà en estadis, una unitat de distància típica de l'època. La conversió del resultat d'Eratòstenes a metres no està clara perquè la mida de l'estadi no era la mateixa en els diversos llocs on s'usava amb aquest nom. Segurament ha estat una coincidència que usant l'estadi egipci la mesura d'Eratòstenes discrepi menys de l'1 per cent del valor real.

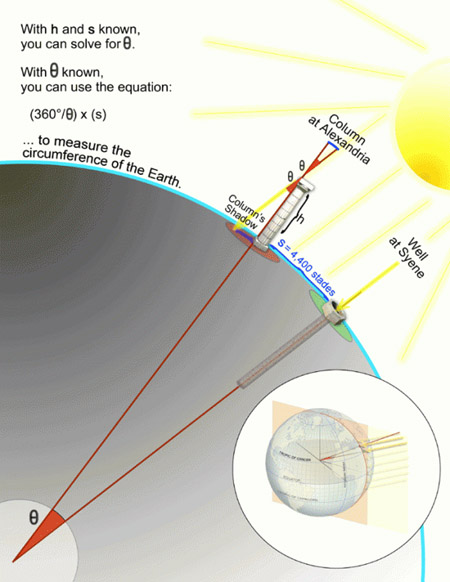
Figura 1. El mètode d'Eratòstenes per mesurar el radi de la Terra.
(Gràfic del NOAA Ocean Service Education's history of geodesy).

El dia 29 de maig de 1919, Arthur Eddington liderava una expedició a l'Illa del Príncep, una illa de cinquanta quilòmetres quadrats, a 200 km de Guinea Equatorial dins el golf, per mesurar la posició aparent de les estrelles al voltant del disc solar, tapat per la lluna durant els cinc minuts de fosca que duraria el primer eclipsi total de Sol d'aquell any.^‡

L'objectiu d'Eddington era confirmar la teoria de la relativitat general d'Einstein. Si la teoria era correcta, les geodèsiques de l'espai estaven modificades pels cossos massius i, en conseqüència, la trajectòria de la llum procedent d'una estrella canviaria quan passés prop del disc solar. Les posicions relatives en que es trobarien les estrelles prop del disc eclipsat canviarien respecte a les posicions mesurades mesos abans, quan fossin visibles de vespre.

El canvi de posició angular entre estrelles seria petit i la incertesa de la mesura s'hauria de determinar molt bé perquè d'ella depenia resoldre si la predicció d'una nova teoria era correcta.

Les mesures fetes sobre les fotografies del camp estel·lar durant l'eclipsi de 1919 marquen la primera comprovació experimental de la teoria de la relativitat general.

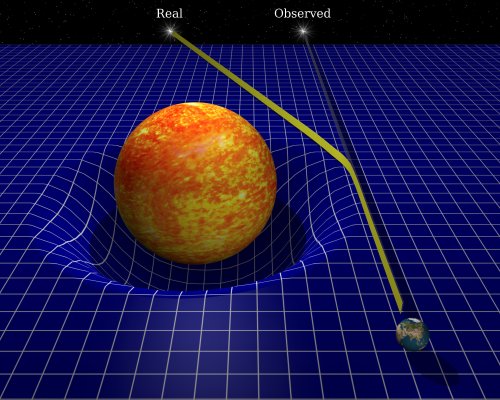
Figura 2. La llum que arriba a la Terra després de passar prop del Sol es desvia i la posició aparent de l'estrella sobre el fons estel·lar canvia. Les escales del gràfic no són reals. (Gràfic de David Jarvis).

El sistema d'unitats emprat en Física es basa en la definició de 7 unitats de mesura per a set magnituds bàsiques. Altres magnituds físiques es defineixen a partir d'elles. Vegeu unitats del Sistema Internacional.

Les constants de gravitació universal, de Coulomb i de Planck són exemples bons.

Isaac Newton enuncià la llei de la gravitació universal. La força entre dos cossos esfèrics és proporcional al producte de les masses i inversament proporcional al quadrat de la distància entre els cossos,

La massa es mesura en kilograms; la distància, en metres; i la força, en newtons (kg m s^–2). La constant de proporcionalitat que dóna el valor concret de la força s'identifica amb la lletra G,

i ha de tenir les unitats N m² kg^–2 = kg^–1 m³ s^–2. El valor de G s'ha de determinar experimentalment.

Charles-Augustin Coulomb enuncià, seguint la llei de la gravitació universal, que la força entre dues càrregues elèctriques puntuals és proporcional al producte de les càrregues i inversament proporcional al quadrat de la distància entre elles,

La càrrega elèctrica es mesura en coulombs (A·s); la distància, en metres; i la força, en newtons (kg m s^–2). Per tant, la constant de proporcionalitat necessària per trobar el valor de la força,

ha de tenir les unitats N m² C^–2. El valor de K s'ha de determinar experimentalment.

L'energia d'un fotó és la constant de Planck multiplicada per la freqüència de la llum. El valor de la constant s'ha de fixar experimentalment. La determinació de la constant de Planck és una pràctica habitual en els laboratoris docents de Física.

Figura 3. Richard Feynmann (Nueva York, 1918 - Los Ángeles, 1988)
(Segell del Servei Postal dels Estats Units, donat per Gerald Skloot, May 2005 a l'American Institute of Physics. Imatge retocada).

Richard Feynmann escrigué:

català » anglès