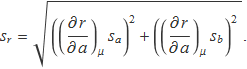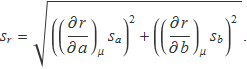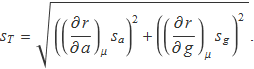Curs ADE: PropEA2

Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.

Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.

Exercicis i problemes

Propagació d'errors aleatoris / 2n^model

1. Suma, Resta i Producte. «

Els valors i els errors estàndards de dues variables independents, expressats en unitats arbitràries, són a = 49.7 ± 1.8 i b = 28.9 ± 0.8. Calcula el valor i l'error estàndard s_r d'una variable r calculada amb les operacions a + b, a – b i a × b. Compara l'error estàndard del resultat de cada operació amb

Solució »

Operació	$s_{r}$	$s_{r}$	$δ_{r}$	$r \pm s_{r}$
$a + b$	$\sqrt{s_{a}^{2} + s_{b}^{2}}$	2	2.5	79 ± 2
$a - b$	$\sqrt{s_{a}^{2} + s_{b}^{2}}$	2	2.5	21 ± 2
$a b$	$\sqrt{a^{2} s_{b}^{2} + b^{2} s_{a}^{2}}$	70	90	1440 ± 70

L'expressió de l'error estàndard s_r mostrat a la segona columna s'ha calculat amb l'expressió

"ade_2.gif"

2. Velocitat relativa «

Dos cotxes van per una carretera seguint una recta (la figura s'ha composat amb un dibuix d'un Fiat 1500 de Viotti Torino). Calcula la probabilitat que la velocitat relativa entre els dos vehicles sigui més gran que 10.0 km/h si el velocímetre d'un cotxe marca 75 km/h i el de l'altre, 65 km/h. Suposa que l'error estàndard en la mesura de la velocitat és de l'1.5%.

Solució »

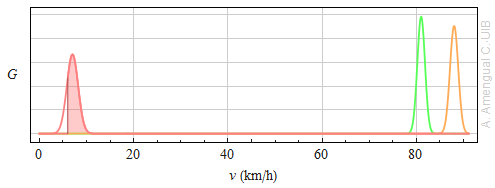
3. Velocitat relativa «

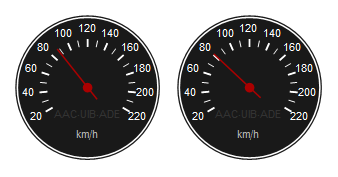
"ade_3.gif"

Calcula la probabilitat que la velocitat relativa entre dos cotxes en una carretera recta sigui més gran que 6.0 km/h si el velocímetre d'un cotxe marca 88 km/h i el de l'altre, 81 km/h. Suposa que l'error estàndard en la mesura de la velocitat és de l'1.0%. Dibuixa les funcions densitat de probabilitat de les velocitats dels dos cotxes i de la velocitat relativa sobre un mateix gràfic, amb l'eix de velocitats des de zero.

Solució »

4. Velocitat relativa «

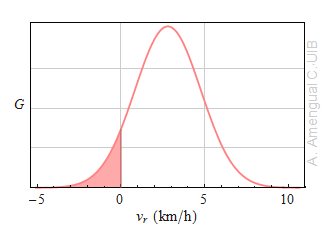
El velocímetre d'un cotxe indica la velocitat amb certa incertesa. Si dos cotxes van per una carretera recta amb velocitats semblants i els conductors es comuniquen la velocitat que veuen en els velocímetres, no poden estar segurs de si s'estan acostant o allunyant.

Suposa que l'error estàndard en la mesura de la velocitat és del 1.5% per calcular la probabilitat que els cotxes s'estiguin acostant quan el velocímetre del cotxe que va devant marca 94.1 km/h i el del cotxe de darrera, 91.3 km/h. Suposa que l'error estàndard en la mesura de la velocitat és de l'1.5%. Expressa la probabilitat en tant per cent amb un decimal i dibuixa esquemàticament la funció densitat de probabilitat de la velocitat relativa.

Solució »

5. Funcions d'una variable «

El valor i l'error estàndard d'una variable és a = 59.5 ± 1.8 (les unitats són arbitràries). Calcula el valor i l'error estàndard s_r d'una variable r calculada amb les operacions indicades a la taula.

Solució oculta » visible

Operació	$s_{r}$	$r \pm s_{r}$
$8 a$	·	·
$- 8 a$	·	·
$a^{2}$	·	·
$\sqrt{a}$	·	·
$\frac{1}{\sqrt{a}}$	·	·

Operació	$s_{r}$	$r \pm s_{r}$
$8 a$	$8 s_{a}$	476 ± 14
$- 8 a$	$8 s_{a}$	-476 ± 14
$a^{2}$	$2 a s_{a}$	3500 ± 200
$\sqrt{a}$	$\frac{s_{a}}{2 \sqrt{a}}$	7.71 ± 0.12
$\frac{1}{\sqrt{a}}$	$\frac{s_{a}}{2 a^{3 / 2}}$	0.130 ± 0.002

L'expressió de l'error estàndard s_r mostrat a la segona columna s'ha calculat amb l'expressió

6. Funcions de dues variables «

Els valors i els errors estàndards de dues variables independents, expressats en unitats arbitràries, són a = 40.8 ± 0.8 i b = 105.0 ± 2.5. Calcula el valor i l'error estàndard s_r d'una variable r calculada amb les operacions indicades a la taula. Compara l'error estàndard amb

Solució oculta » visible

Operació	$s_{r}$	$s_{r}$	$δ_{r}$	$r \pm s_{r}$
$\frac{a}{b}$	·	·	·	·
$a \sqrt{b}$	·	·	·	·
$a + \sqrt{b}$	·	·	·	·
$\frac{a}{\sqrt{b}}$	·	·	·	·
$\sqrt{\frac{a}{b}}$	·	·	·	·

Operació	$s_{r}$	$s_{r}$	$δ_{r}$	$r \pm s_{r}$
$\frac{a}{b}$	$\sqrt{\frac{a^{2} s_{b}^{2}}{b^{4}} + \frac{s_{a}^{2}}{b^{2}}}$	0.012	0.017	0.389 ± 0.012
$a \sqrt{b}$	$\sqrt{\frac{a^{2} s_{b}^{2}}{4 b} + b s_{a}^{2}}$	10	13	420 ± 10
$a + \sqrt{b}$	$\sqrt{s_{a}^{2} + \frac{s_{b}^{2}}{4 b}}$	0.8	0.9	51.0 ± 0.8
$\frac{a}{\sqrt{b}}$	$\sqrt{\frac{a^{2} s_{b}^{2}}{4 b^{3}} + \frac{s_{a}^{2}}{b}}$	0.09	0.13	3.98 ± 0.09
$\sqrt{\frac{a}{b}}$	$\sqrt{\frac{a s_{b}^{2}}{4 b^{3}} + \frac{s_{a}^{2}}{4 a b}}$	0.01	0.014	0.62 ± 0.01

L'expressió de l'error estàndard s_r mostrat a la segona columna s'ha calculat amb l'expressió

"ade_8.gif"

7. Període d'un pèndol simple «

La longitud d'un pèndol simple és a = 0.96 ± 0.03 m. Calcula el període de les oscil·lacions de petita amplitud si l'acceleració de la gravetat val g = 9.8 ± 0.3 m/s². Les incerteses donades són els errors estàndard d'a i g, respectivament. Compara l'error estàndard del període amb

Solució oculta » visible

Període	$s_{T}$	$s_{T}$	$δ_{T}$	$T \pm s_{T}$
$2 π \sqrt{\frac{a}{g}}$	·	·	·	·

Període	$s_{T}$	$s_{T}$	$δ_{T}$	$T \pm s_{T}$
$2 π \sqrt{\frac{a}{g}}$	$\sqrt{\frac{π^{2} a s_{g}^{2}}{g^{3}} + \frac{π^{2} s_{a}^{2}}{a g}}$	0.04	0.06	1.97 ± 0.04

L'expressió de l'error estàndard s_T mostrat a la segona columna s'ha calculat amb l'expressió

"ade_10.gif"

8. Llançament amb fregament «

L'altura màxima a la que arriba una esfera llançada amb un angle α i velocitat inicial v₀ amb una força de fregament proporcional a la velocitat, Q = –m b v, és

a) Si les incerteses sobre b = 0.0946 s^–1 i l'acceleració de la gravetat g = 9.800 m/s² es poden negligir, quina és l'altura màxima a la que arribarà l'objecte si v₀ = 35.3 ± 0.3 m/s i l'angle de llançament en graus val 53.705 ± 0.006?

b) Què ha afectat més a la incertesa sobre l'altura màxima, la incertesa sobre la velocitat inicial o la incertesa sobre l'angle de llançament?

Solució »

9. Energia d'un satèl·lit «

Un satèl·lit de 1301.7 ± 0.4 kg es mou en una órbita circular de 3694.2 ± 0.6 km d’altura sobre la Terra.

a) Calcula l'energia potencial amb la incertesa.

b) Quina és la velocitat del satèl·lit?

Dades: M_T = 5.9736 10²⁴ kg, R_T = 6378 ± 20 km.

Solució »