
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Presentació de resultats
Incertesa relativa
Introducció «
En el tema anterior s'ha mostrat que la incertesa sobre un valor numèric determina el nombre de xifres significatives amb les que s'ha d'escriure el valor quan es doni com a resultat. Si s'obté x = 123.76 amb una incertesa de 0.2, s'ha d'escriure x = 123.8 ± 0.2; però si la incertesa és 0.04, s'ha d'escriure x = 123.76 ± 0.04. El quocient entre el valor de la incertesa i el valor numèric és cinc vegades més petit en el segon exemple que en el primer. Aquest quocient defineix la incertesa relativa. Una incertesa de 0.04 por ser acceptable o inacceptable depenent del valor numèric al que estigui associada. Com més gran és l'error relatiu, menys fiable és el valor numèric.
El càlcul de l'error relatiu s'usarà a la darrera secció d'aquest tema per justificar el criteri presentat en el tema anterior per arrodonir les incerteses amb una o dues xifres significatives.
Expressió d'un resultat amb la incertesa relativa
 «
«
La incertesa relativa percentual sobre una variable x es calcula amb el valors de la variable i de la incertesa sense arrodonir usant l'expressió
![]()
S'han d'usar els valors originals de x i δx sense arrodonir per calcular la incertesa relativa.
El valor de la variable x s'escriurà per donar el resultat arrodonit segons els criteris indicats en els apartats anteriors. El valor de la incertesa relativa s'arrodonirà per donar una xifra significativa o dues quan les xifres significatives formin alguna de les parelles
10, 11, 12, 13, 14, 15, 16, 17, 18 o 25.
A la taula següent es mostren alguns exemples. També s'hi mostra la manera amb que s'ha d'escriure un resultat si es vol donar amb la incertesa absoluta i la incertesa relativa.
| valor | incertesa | inc. abs. | inc. rel. | abs. & rel. |
| 25.64 | 4.42 | 26 ± 4 | 26 ± 17 % | 26 ± 4 (17 %) |
| 85.12 | 16.49 | 85 ± 16 | 85 ± 20 % | 85 ± 16 (20 %) |
| 74.16 | 6.37 | 74 ± 6 | 74 ± 9 % | 74 ± 6 (9 %) |
| 27.11 | 3.82 | 27 ± 4 | 27 ± 14 % | 27 ± 4 (14 %) |
| 20.84 | 3.77 | 21 ± 4 | 21 ± 18 % | 21 ± 4 (18 %) |
| 74.28 | 6.79 | 74 ± 7 | 74 ± 9 % | 74 ± 7 (9 %) |
| 52.15 | 8.37 | 52 ± 8 | 52 ± 16 % | 52 ± 8 (16 %) |
| 35.12 | 2.53 | 35.0 ± 2.5 | 35.0 ± 7 % | 35.0 ± 2.5 (7 %) |
| 70.48 | 3.42 | 70 ± 3 | 70 ± 5 % | 70 ± 3 (5 %) |
| 71.22 | 12.78 | 71 ± 13 | 71 ± 18 % | 71 ± 13 (18 %) |
Taula 1. Exemples de l'expressió de diversos valors amb la incertesa relativa.
Canvi relatiu quan s'arrodoneix
 «
«
La reducció o l'agument d'una incertesa δx per l'arrodoniment es quantifica calculant la variació relativa amb la fórmula
![]()
on δX és la incertesa arrodonida. Per exemple, si δx = 0.314 unitats, l'arrodoniment a δX = 0.3 redueix la incertesa en un quatre per cent:
![]()
Si no s'usassin dues xifres significatives quan la primera és 1, la discrepància seria massa gran, per exemple δx = 14.9 unitats s'arrodoniria a δX = 10 i la variació seria de quasi el cinquanta per cent:
![]()
La Fig. 1 és el canvi relatiu quan s'arrodoneix δx per a valors entre 0.1 i 1.05. La figura mostra que la incertesa arrodonida amb el criteri que se seguirà mai discrepa més del 15% del valor sense arrodonir.
El domini de la figura és l'interval [0.1, 1.05) però es pot multiplciar per qualsevol potència de deu i εr no canviarà. El canvi relatiu amb l'arrodoniment de δx × 10n per a qualsevol n és el mateix que el de δx perquè el factor 10n es cancel·la en el quocient que dóna εr.
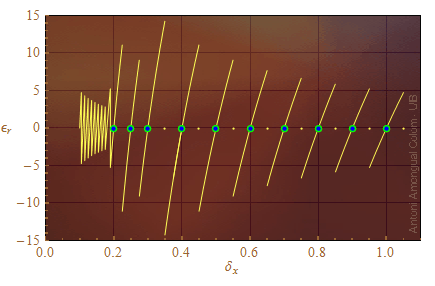
Figura 1. Canvi relatiu en el valor d'una incertesa dins [0.1, 1.05).
